Student handout: Vector Differential--Rectangular

Surfaces/Bridge Workshop 2023

In this introductory lecture/SWBQ, students are given a picture as a guide. They then write down an algebraic expression for the vector differential in rectangular coordinates for coordinate equals constant paths.

This activity can be done as a mini-lecture/SWBQ as an introduction to Vector Differential--Curvilinear where students find the vector differential in cylindrical and spherical coordinates..

Vector Differential: Rectangular Coordinates:

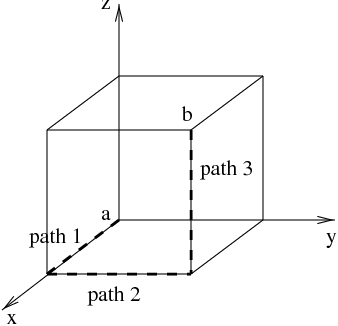
Find the general form for \(d\vec{r}\) in rectangular coordinates by determining \(d\vec{r}\) along the specific paths in the figure below.

  • Path 1: \[d\vec{r}=\hspace{35em}\]
  • Path 2: \[d\vec{r}=\hspace{35em}\]
  • Path 3: \[d\vec{r}=\hspace{35em}\]

If all three coordinates are allowed to change simultaneously, by an infinitesimal amount, we could write this \(d\vec{r}\) for any path as:

\[d\vec{r}=\hspace{35em}\]

This is the general line element in rectangular coordinates.

Figure 1: \(d\vec{r}\) in rectangular coordinates
Keywords
vector differential rectangular coordinates math
Learning Outcomes