Quantum Fundamentals: NoTerm-2021
HW 7 : Due 3/3 Wed

1. Spin One Interferometer Brief S0 4112S

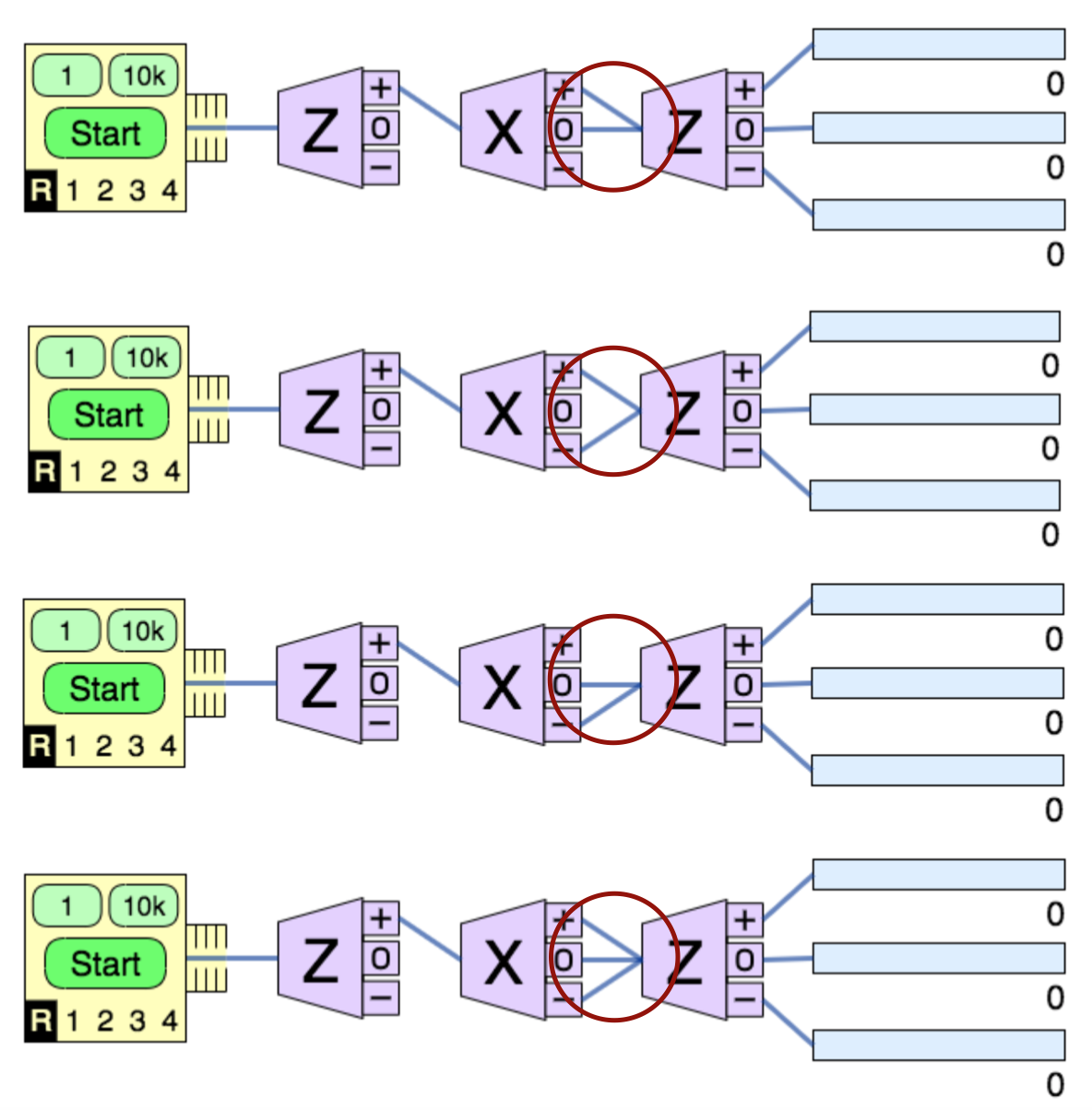
   Consider a spin 1 interferometer which prepares the state as \(| 1\rangle\), then sends this state through an \(S_x\) apparatus and then an \(S_z\) apparatus. For the four possible cases where a pair of beams or all three beams from the \(S_x\) Stern-Gernach analyzer are used, calculate the probabilities that a particle entering the last Stern-Gerlach device will be measured to have each possible value of \(S_z\). Compare your theoretical calculations to results of the simulation. Make sure that you explicitly discuss your choice of projection operators.

   Note: You do not need to do the first case, as we have done it in class.
   

2. Completeness Relation Change of Basis S0 4112S

   1. Given the polar basis kets written as a superposition of Cartesian kets \begin{eqnarray*} \left|{\hat{s}}\right\rangle &=& \cos\phi \left|{\hat{x}}\right\rangle + \sin\phi \left|{\hat{y}}\right\rangle \\ \left|{\hat{\phi}}\right\rangle &=& -\sin\phi \left|{\hat{x}}\right\rangle + \cos\phi \left|{\hat{y}}\right\rangle \end{eqnarray*}

      Find the following quantities: \[\left\langle {\hat{x}}\middle|{\hat{s}}\right\rangle ,\quad \left\langle {\hat{y}}\middle|{{\hat{s}}}\right\rangle ,\quad \left\langle {\hat{x}}\middle|{\hat{\phi}}\right\rangle ,\quad \left\langle {\hat{y}}\middle|{\hat{\phi}}\right\rangle \]

   2. Given a vector written in the polar basis \[\left|{\vec{v}}\right\rangle = a\left|{\hat{s}}\right\rangle + b\left|{\hat{\phi}}\right\rangle \] where \(a\) and \(b\) are known. Find coefficients \(c\) and \(d\) such that \[\left|{\vec{v}}\right\rangle = c\left|{\hat{x}}\right\rangle + d\left|{\hat{y}}\right\rangle \] Do this by using the completeness relation: \[\left|{\hat{x}}\right\rangle \left\langle {\hat{x}}\right| + \left|{\hat{y}}\right\rangle \left\langle {\hat{y}}\right| = 1\]
   3. Using a completeness relation, change the basis of the spin-1/2 state \[\left|{\Psi}\right\rangle = g\left|{+}\right\rangle + h\left|{-}\right\rangle \] into the \(S_y\) basis. In otherwords, find \(j\) and \(k\) such that \[\left|{\Psi}\right\rangle = j\left|{+}\right\rangle _y + k\left|{-}\right\rangle _y\]
3. Phase 2 S0 4112S Consider the three quantum states: \[\left\vert \psi_1\right\rangle = \frac{4}{5}\left\vert +\right\rangle+ i\frac{3}{5} \left\vert -\right\rangle\] \[\left\vert \psi_2\right\rangle = \frac{4}{5}\left\vert +\right\rangle- i\frac{3}{5} \left\vert -\right\rangle\] \[\left\vert \psi_3\right\rangle = -\frac{4}{5}\left\vert +\right\rangle+ i\frac{3}{5} \left\vert -\right\rangle\]
   1. For each quantum state \(\left|{\psi_i}\right\rangle \) given above, calculate the probabilities of obtaining \(+\frac{\hbar}{2}\) and \(-\frac{\hbar}{2}\) when measuring the spin component along the \(x\)-, \(y\)-, and \(z\)-axes.
   2. Look For a Pattern (and Generalize): Use your results from \((a)\) to comment on the importance of the overall phase and of the relative phases of the quantum state vector.