Quantum Fundamentals: NoTerm-2021
HW 5 : Due 2/24 Wed
- Chained Stern-Gerlach
S0 4110S
Consider the Stern-Gerlach set-up shown, with a thermal oven” source, and some state vectors associated with various analyzer outputs:
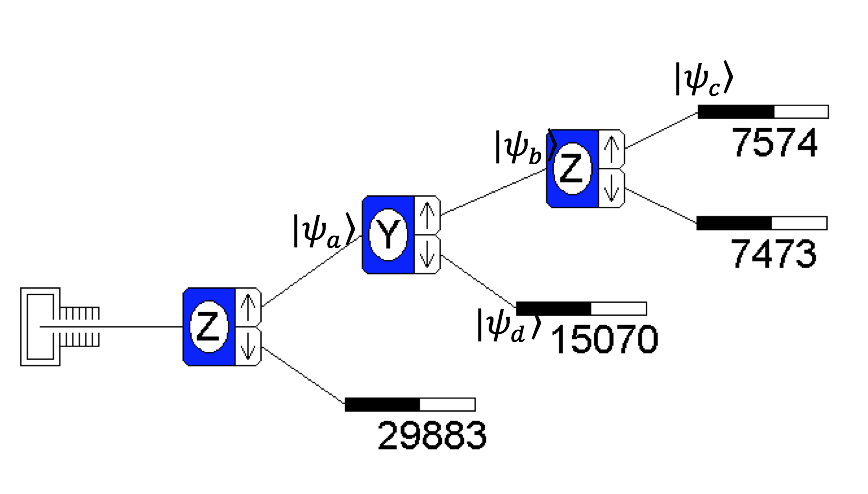
How many particles were released from the oven? Calculate it exactly but also make a more conceptual/quick way to determine the (approximate, likely) answer. Describe both ways.
Write down Dirac notation expressions for \(|\Psi_a \rangle\), \(|\Psi_b \rangle\), \(|\Psi_c \rangle\) and \(|\Psi_d \rangle\) in the \(S_z\)-basis.
Student A says, “While going through the y-analyzer (Analyzer 2), the y-analyzer changes its incoming particles from being all z+ to an output which is a mixture of half of the particles being in the z+ state and half being in the z- state. That's why the farthest right z-analyzer (call it Analyzer 3) measures half z+ and half z-.”
Student B says, “No that's not right, all the particles entering Analyzer 3 are in the same state: they are in both the z+ and z- at the same time, they are all in a state that is a specific superposition of z+ and z- states, which is \(|\Psi_b\rangle\).”
Student C says, “There's no way to tell the difference between those two cases. So your argument doesn't matter in practice.”
Student D states, “Student B is right (sorry for the formality, B), and A and C are wrong, especially C.”
Describe a simple experiment (or experiments) and use a clear logical argument to show that Student D is correct (including the idea that C is wrong). Draw diagrams to make your case easier to comprehend. (Hint: Figure 1.12 in McIntyre might be helpful.)
- Orthogonal Brief
S0 4110S
Consider the quantum state: \[\left\vert \psi\right\rangle = \frac{1}{\sqrt{3}}\left\vert +\right\rangle+ i\frac{\sqrt{2}}{\sqrt{3}} \left\vert -\right\rangle\]
Find the normalized vector \(\vert \phi\rangle\) that is orthogonal to it.
- Phase in Quantum States
S0 4110S
In quantum mechanics, it turns out that the overall phase for a state does not have any physical significance. Therefore, you will need to become quick at rearranging the phase of various states. For each of the vectors listed below, rewrite the vector as an overall complex phase times a new vector whose first component is real and positive. \[\left|D\right\rangle\doteq \begin{pmatrix} 7e^{i\frac{\pi}{6}}\\ 3e^{i\frac{\pi}{2}}\\ -1\\ \end{pmatrix}\\ \left|E\right\rangle\doteq \begin{pmatrix} i\\ 4\\ \end{pmatrix}\\ \left|F\right\rangle\doteq \begin{pmatrix} 2+2i\\ 3-4i\\ \end{pmatrix} \]
- Measurement Probabilities
S0 4110S
A beam of spin-\(\frac{1}{2}\) particles is prepared in the initial state \[ \left\vert \psi\right\rangle = \sqrt{\frac{2}{5}}\; |+\rangle_x - \sqrt{\frac{3}{5}}\; |-\rangle_x \](Note: this state is written in the \(S_x\) basis!)
- What are the possible results of a measurement of \(S_x\), with what probabilities?
Repeat part a for measurements of \(S_z\).
- Suppose you start with a particle in the state given above, measure \(S_x\), and happen to get \(+\hbar /2\). You then take that same particle and measure \(S_z\). What are the possible results and with what probability would you measure each possible result?