Quantum Fundamentals: NoTerm-2021
HW 2 : Due 2/12 Fri
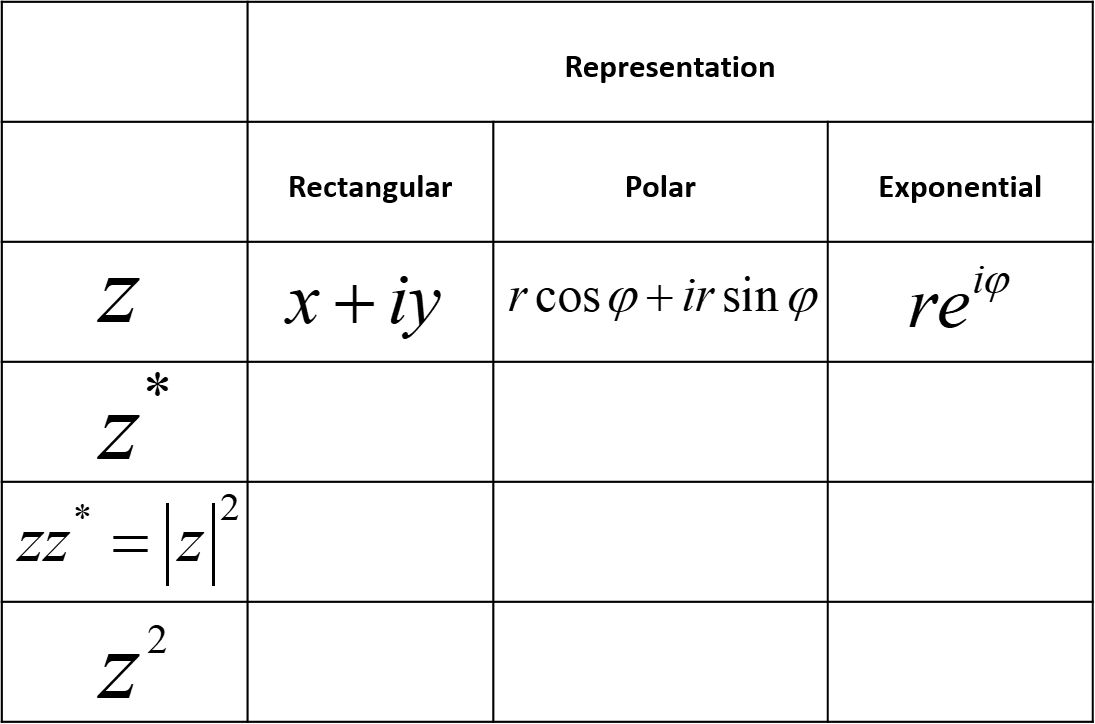
- Representations of Complex Numbers--Table
S0 4107S
Fill out the table above that asks you to do several simple complex number calculations in rectangular, polar, and exponential representations.
- Graphs of the Complex Conjugate
S0 4107S
For each of the following complex numbers, determine the complex conjugate, square, and norm. Then, plot and clearly label each \(z\), \(z^*\), and \(|z|\) on an Argand diagram.
- \(z_1=4i-3\)
- \(z_2=5e^{-i\pi/3}\)
- \(z_3=-8\)
- In a few full sentences, explain the geometric meaning of the complex conjugate and norm.
- Euler's Formula I
S0 4107S
- Use Euler's formula \(e^{i\phi}=\cos\phi+i\sin\phi\) and its complex conjugate to find formulas for \(\sin\phi\) and \(\cos\phi\). In your physics career, you will often need to read these formula “backwards,” (i.e. notice one of these combinations of exponentials in a sea of other symbols and say, Ah ha! that is \(\cos\phi\)). So, pay attention to the result of the homework problem!
Show that Euler's formula:
\[e^{i\phi} = \cos\phi +i \sin\phi\]
is true, by comparing the power series for the various terms.
- Pauli Practice
S0 4107S
The Pauli spin matrices \(\sigma_x\), \(\sigma_y\), and \(\sigma_z\) are
defined by:
\[\sigma_x=
\begin{pmatrix}
0&1\\ 1&0\\
\end{pmatrix}
\hspace{2em}
\sigma_y=
\begin{pmatrix}
0&-i\\ i&0\\
\end{pmatrix}
\hspace{2em}
\sigma_z=
\begin{pmatrix}
1&0\\ 0&-1\\
\end{pmatrix}
\]
These matrices are related to angular momentum in
quantum mechanics. Prove, and become familiar with, the identities
listed below.
- Show that each of the Pauli matrices is hermitian. (A matrix is hermitian if it is equal to its hermitian adjoint.)
- Show that the determinant of each of the Pauli matrices is \(-1\).
- Show that \(\sigma_i^2={\cal I}\) for each of the Pauli matrices, i.e. for \(i\in\left\{x,y,z\right\}\).
- Pauli
S0 4107S
The Pauli spin matrices \(\sigma_x\), \(\sigma_y\), and \(\sigma_z\) are
defined by:
\[\sigma_x=
\begin{pmatrix}
0&1\\ 1&0\\
\end{pmatrix}
\hspace{2em}
\sigma_y=
\begin{pmatrix}
0&-i\\ i&0\\
\end{pmatrix}
\hspace{2em}
\sigma_z=
\begin{pmatrix}
1&0\\ 0&-1\\
\end{pmatrix}
\]
These matrices are related to angular momentum in
quantum mechanics. Prove, and become familiar with, the identities
listed below.
- Show that \(\sigma_x \sigma_y = i\sigma_z\) and \(\sigma_y \sigma_x = -i\sigma_z\). (Note: These identities also hold under a cyclic permutation of \(\left\{x,y,z\right\}\), e.g. \(x\rightarrow y\), \(y\rightarrow z\), and \(z\rightarrow x\)).
- The commutator of two matrices \(A\) and \(B\) is defined by \(\left[A, B\right]\buildrel \rm def \over = AB-BA\). Show that \(\left[\sigma_x, \sigma_y\right] = 2i\sigma_z\). (Note: This identity also holds under a cyclic permutation of \(\left\{x,y,z\right\}\), e.g. \(x\rightarrow y\), \(y\rightarrow z\), and \(z\rightarrow x\)).
- The anti-commutator of two matrices \(A\) and \(B\) is defined by \(\left\{A, B\right\}\buildrel \rm def \over = AB+BA\). Show that \(\left\{\sigma_x, \sigma_y\right\} = 0\). (Note: This identity also holds under a cyclic permutation of \(\left\{x,y,z\right\}\), e.g. \(x\rightarrow y\), \(y\rightarrow z\), and \(z\rightarrow x\)).