Quantum Fundamentals: NoTerm-2021
HW 1 : Due 2/10 Wed
- Ph425 Student Info
S0 4105S
If this is your first course with me: Please send me an e-mail (with subject “RE: Ph425 HW1”- do not put this info in your written homework solutions) with the following information:
- What name would you like to use in class?
- What are your pronouns?
- What is a cool fact about you?
- Is there anything else you'd like me to know about you? (background that might be relevant, concerns about the course, how you've been personally impacted by COVID-19, struggles with motivation/depression, etc).
If you have taken a course with me before: welcome back! If you'd like to give me an update with what's going on with you (a cool new fact, concerns about the course, how you've been personally impacted by COVID-19, struggles with motivation/depression, etc), send me an e-mail with the subject heading above. This is optional, but I'd like to know what's going on with you!
- Circle Trigonometry
S0 4105S
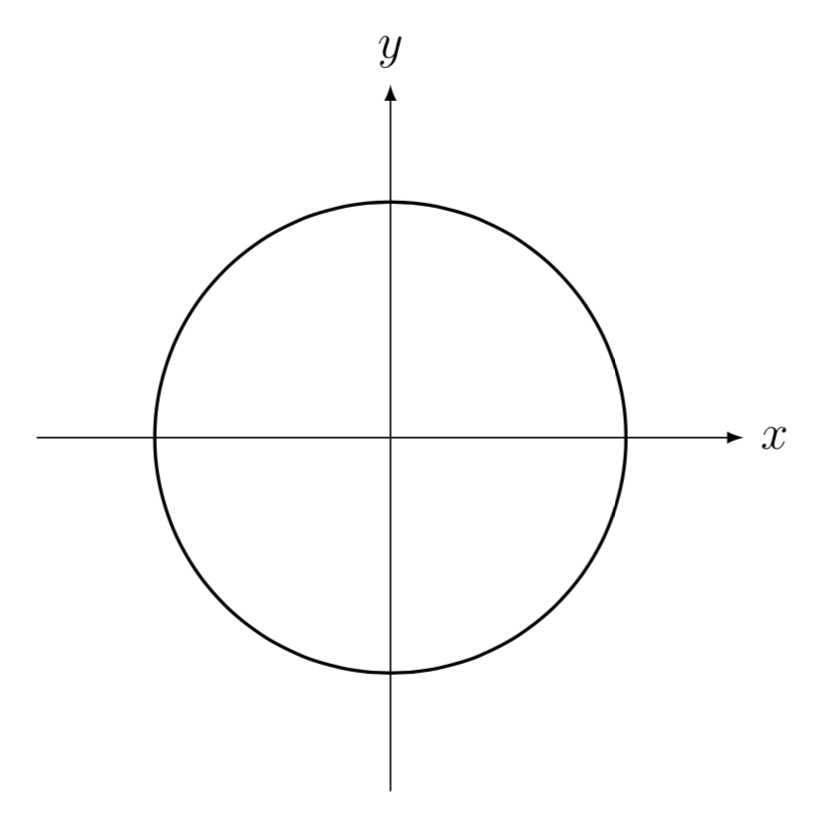
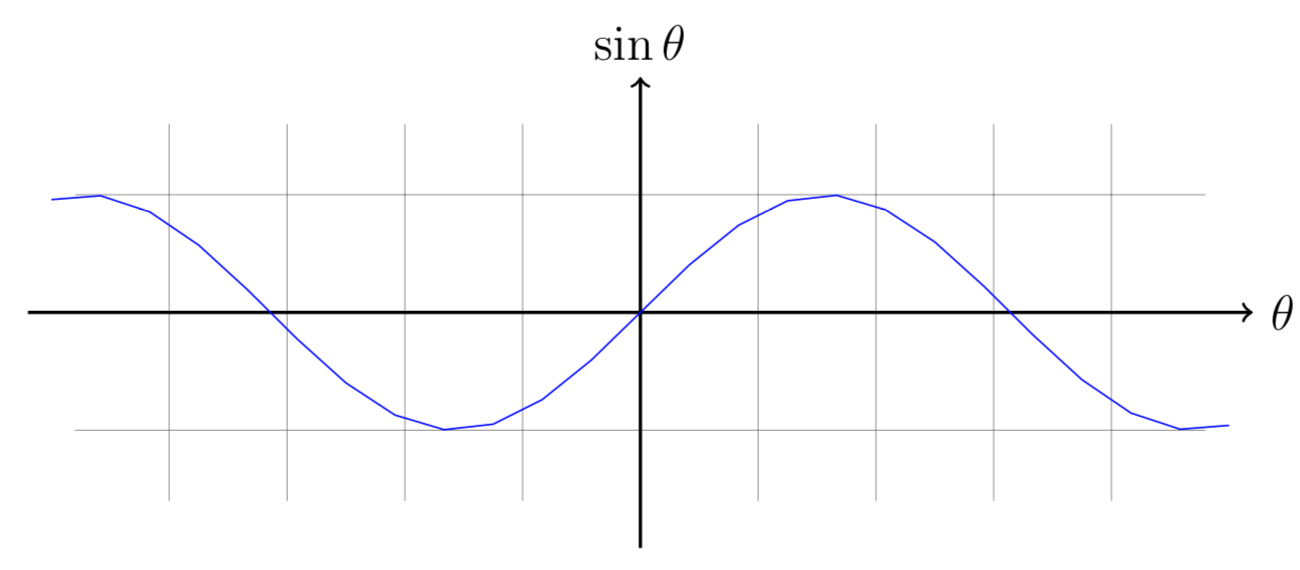
On the following diagrams, mark both \(\theta\) and \(\sin\theta\) for \(\theta_1=\frac{5\pi}{6}\) and \(\theta_2=\frac{7\pi}{6}\). Write one to three sentences about how these two representations are related to each other. (For example, see: this PHET)
- Matrix Refresher
S0 4105S
Calculate the following quantities for the matrices:
\[A\doteq
\begin{pmatrix}
1&0&0\\ 0&0&1\\ 0&-1&0\\
\end{pmatrix}
\hspace{2em}
B\doteq
\begin{pmatrix}
a&b&c\\ d&e&f\\ g&h&j\\
\end{pmatrix}
\hspace{2em}
C\doteq
\begin{pmatrix}
\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\\
\end{pmatrix}
\]
and the vector:
\[\left|D\right\rangle\doteq
\begin{pmatrix}
1\\ i\\ -1\\
\end{pmatrix}
\hspace{2em}
\]
- \(AB\)
- \({\rm tr} (B)\)
- \(A\vert D\rangle\)
- \(\det(\lambda{\cal I}-A)\) where \(\lambda\) is a scalar.
- \(C^{-1}\) (Hint: Geometrically, what is the \(C\) transformation? What transformation undoes what \(C\) does?)
- Complex Arithmetic: Rectangular Form
S0 4105S
For the complex numbers \(z_1=3-4i\) and \(z_2=7+2i\), compute:
- \(z_1-z_2\)
- \(z_1 \, z_2\)
- \(\frac{z_1}{z_2}\)