Consider the following normalized quantum state on a unit ring: \begin{equation} \Phi(\phi)=\sqrt\frac{8}{3 \pi r_0} \sin^{2}\left( 3\,\phi \right)\cos \left( \phi \right) \end{equation}

1. Translate this state into eigenfunction, bra/ket, and matrix representations. Remember that you can use any of these representations in the following calculations.
2. What is the expectation value of \(L_z\) in this state?

3. The wave function and it's probability density are plotted below. (I have set \(r_0=1\) to make the plotting easier). What features of these graphs (if any) tell you the expectation value of \(L_z\) in this state?

   
   

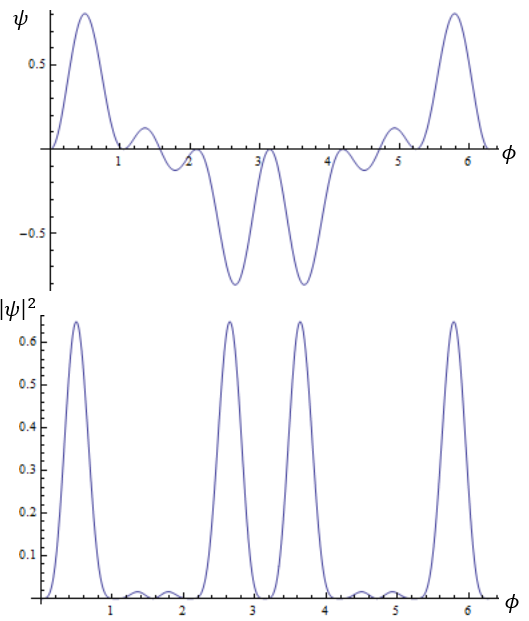
4. What is the probability that the particle can be found in the region \(0<\phi< \frac{\pi}{4}\)? Repeat your calculation in the region \(\frac{\pi}{4}<\phi< \frac{3 \pi}{4}\)?