Student handout: Divergence and Curl

Vector Calculus II 2021
Choose a vector field \(\boldsymbol{\vec{F}}\) from the first column below. Choose a small loop \(C\) (that is, a simple, closed, positively-oriented curve) which does not go around the origin.
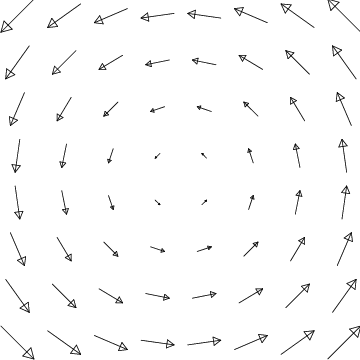
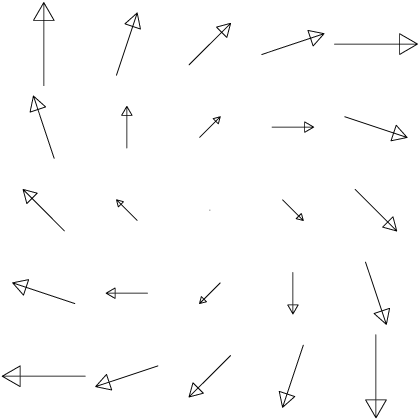
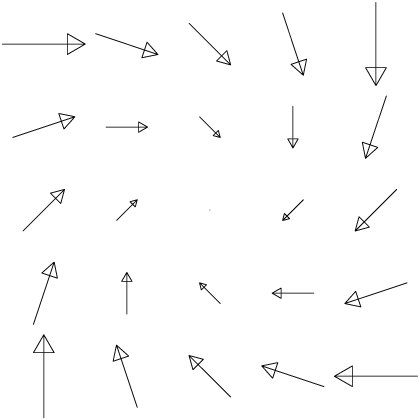
  • Is \(\oint\boldsymbol{\vec{F}}\cdot d\boldsymbol{\hat{r}}\) positive, negative, or zero?
  • Will a paddlewheel spin if placed inside your loop, and, if so, which way?

  • Do you think \(\nabla\times\boldsymbol{\vec{F}}\) is zero or nonzero inside your loop?

    Explain.

  • Compute \(\nabla\times\boldsymbol{\vec{F}}\). Did you guess right? Explain.
  • Is \(\oint\boldsymbol{\vec{F}}\cdot\boldsymbol{\hat{n}}\,ds\) positive, negative, or zero? (\(\boldsymbol{\hat{n}}\) is the outward pointing normal vector to \(C\).)
  • Is the net flow outwards across your loop positive, negative, or zero?
  • Do you think \(\nabla\cdot\boldsymbol{\vec{F}}\) is zero or nonzero inside your loop? Explain.
  • Compute \(\nabla\cdot\boldsymbol{\vec{F}}\). Did you guess right? Explain.
  • Repeat the above steps for vector fields \(\boldsymbol{\vec{G}}\) and \(\boldsymbol{\vec{H}}\) chosen from the second and third columns.
\(-y\,\boldsymbol{\hat{x}}+x\,\boldsymbol{\hat{y}}\) \((x+y)\,\boldsymbol{\hat{x}}+(y-x)\,\boldsymbol{\hat{y}}\) \(e^{-y^2}\,\boldsymbol{\hat{y}}\)
 
\(x\,\boldsymbol{\hat{x}}+y\,\boldsymbol{\hat{y}}\) \((y-x)\,\boldsymbol{\hat{x}}-(x+y)\,\boldsymbol{\hat{y}}\) \(e^{-x^2}\,\boldsymbol{\hat{y}}\)
Keywords
Learning Outcomes