Student handout: Velocity and Acceleration in Polar Coordinates
Central Forces 2021
Use geometry to find formulas for velocity and acceleration in polar coordinates.
- group Small Group Activity 10 min. Tabletop Whiteboard with markers,A handout for each student Student handout (PDF)
What students learn
Students derive expressions for the velocity and acceleration in polar coordinates. Along the way, students discover:
- Since \(\hat{r}\) and \(\hat{\phi}\) are functions of position in space, if these basis vectors are being used to describe the position of a particle as a function of time, then \(\hat{r}\) and \(\hat{\phi}\) can also depend on time.
- To find how \(\hat{r}\) and \(\hat{\phi}\) depend on time, it is easiest to express them in terms of rectangular basis vectors \(\hat{x}\) and \(\hat{y}\), which do not depend on either position or time.
On the figure below, draw \(\hat{s}\) and \(\hat{\phi}\) at \(P\).
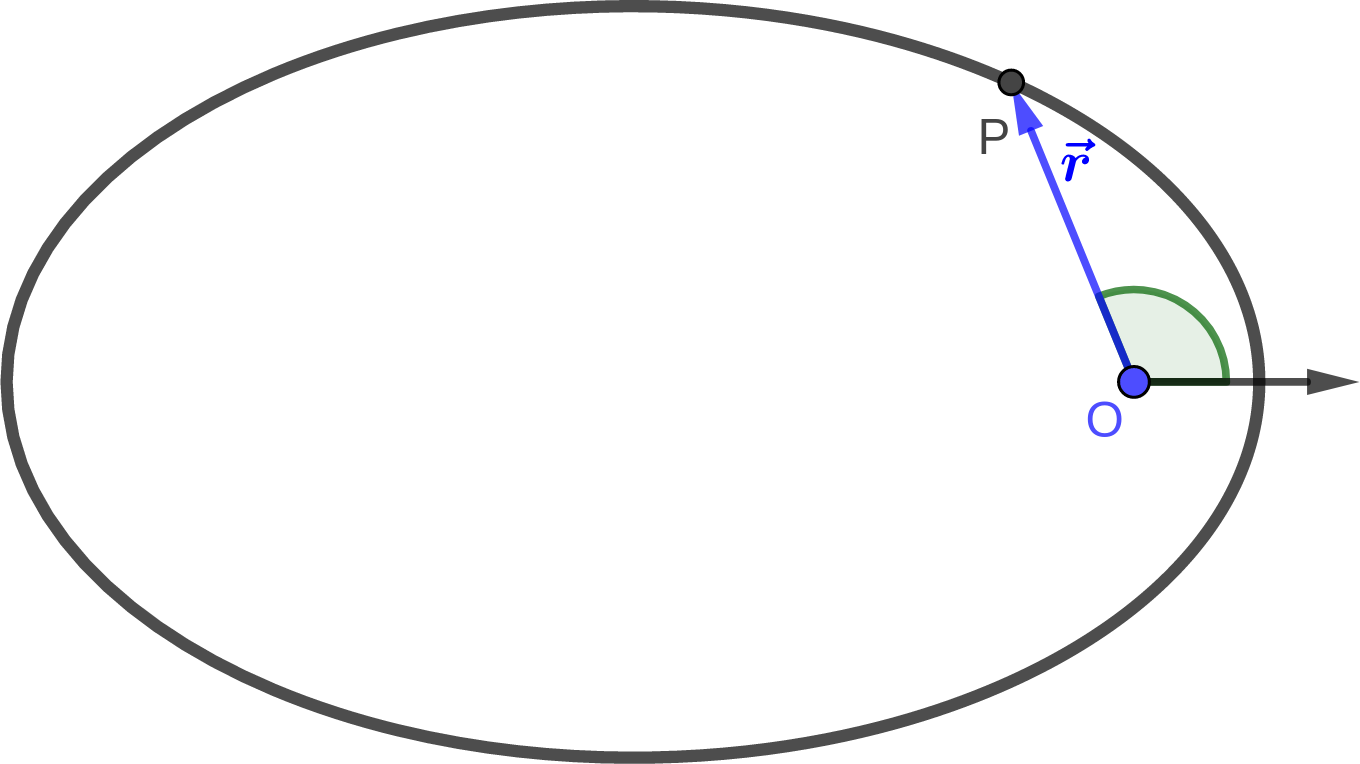
- Find \(\frac{d}{dt}\hat{s}\) and \(\frac{d}{dt}\hat{\phi}\) in terms of \(\hat{s}\) and \(\hat{\phi}\).
- Find \(\vec{v}\) in terms of \(\hat{s}\) and \(\hat{\phi}\).
- Keywords
- Learning Outcomes
-