Periodic Systems: NoTerm-2022
HW 8 : Due Day 22 12/2

1. Molecular Orbitals of Model Hydrogen Ion S0 4506S

   In class we have solved the molecular orbitals of an ionized model hydrogen molecule using LCAO approximation. We found there are two orbitals, corresponding to even and odd wave functions.

   Now, directly solve (not LCAO) the energy eigenvalue problem of \(H=\frac{p^2}{2m}+V\), where \(V=-\gamma\delta(x+a)-\gamma\delta(x-a)\), where \(2a\) is the separation of our model \(H\) nucleus.

   1. Write an ansatz for bound state with energy \(E<0\). Because the potential is symmetric (even), you should expect to have an even and an odd wave function.
   2. In the above ansatz you would have several unknowns. To solve the unknowns you would need to apply continuity conditions. Express the continuity conditions using the ansatz you made in the last question.
   3. (extra credit) You will not be able to solve the equations analytically, but you can learn the important features of them by graphs. In particular, if you find one of the unknowns, say \(\beta\) satisfies \(f(\beta)=g(\beta)\), where \(f\) and \(g\) are functions you derived from the last question, you may plot \(f(\beta)\) and \(g(\beta)\) and the solution would be the intersection point. Try this method (show the graphs) to solve for the energies of the eigenstates. You may estimate the value of \(\gamma\) as the ionization energy of a single hydrogen atom.

   4. (extra credit) Sketch the energies as a function of \(x\), you should have two curves. Which state contributes to the formation of the molecule?

      

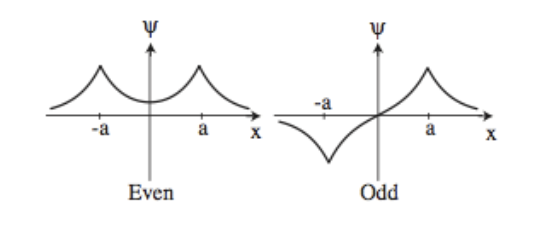
      The even state contributes to the formation of the molecule because there is a higher probability density in the region between the nuclei.