Central Forces: Spring-2025
HW 04 (SOLUTION): Due W2 D5
- Sun vs. Jupiter
S1 5238S
Gain experience with the relative sizes of objects and distances in the Solar System. Gain experience with realistic reduced masses.
Calculate the following quantities:
-
Find \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) and \(\mu\) for the
Sun-Earth system. Compare \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) to
the radius of the Sun and to the distance from the Sun to the Earth.
Compare \(\mu\) to the mass of the Sun and the mass of the Earth.
Our answer at the end should be a direct comparison (for example, a ratio) between radii and a different comparison between masses. Sun\(\leftrightarrow\)Earth \begin{align*} |\vec r_{\rm s}-\vec r_{\rm e}| &= 148\times 10^9 m\\ R_{\rm s} &= \hbox{radius of Sun}\\ &= 7\times 10^8 m\\ m_{\rm s} &= \hbox {mass of Sun}\\ &= 2\times 10^{30} kg\\ m_{\rm e} &= \hbox {mass of Earth}\\ &= 5.98\times 10^{24} kg \end{align*}
Therefore: \begin{equation*} \mu=\frac{m_{\rm e}m_{\rm s}}{ m_{\rm e}+m_{\rm s}}=5.98\times 10^{24}kg\approx m_{\rm e}=3\times 10^{-6}m_{\rm s} \end{equation*} and: \begin{align*} |{\vec r}_{\rm s}-{\vec r}_{\rm cm}| &= \left\vert{\vec r}_{\rm s}- \frac{m_{\rm e}{\vec r}_{\rm e} + m_{\rm s}{\vec r}_{\rm s}}{m_{\rm e} +m_{\rm s}}\right\vert\\ &= \frac{m_{\rm e}}{ m_{\rm e} +m_{\rm s}}|{\vec r}_{\rm s}-{\vec r}_{\rm e}|\\ &= 4.425\times 10^5m \end{align*}
Comparisons: \begin{align*} \frac{|{\vec r}_{\rm s}-{\vec r}_{\rm cm}|}{R_{\rm s}} &=& 6.3\times 10^{-4}\\ \frac{|{\vec r}_{\rm s}-{\vec r}_{\rm cm}|}{|{\vec r}_{\rm s}-{\vec r}_{\rm e}|} &=& 3.0\times 10^{-6} \end{align*} i.e. The center-of-mass, about which the sun and earth both rotate, is well inside the sun itself.
-
Repeat the calculation for the Sun-Jupiter system.
Sun\(\leftrightarrow\)Jupiter \begin{align*} |\vec r_{\rm s}-\vec r_{\rm j}| &= 778\times 10^9 m\\ R_{\rm s} &= \textrm{radius of Sun}\\ &= 7\times 10^8 m\\ m_{\rm s} &= \textrm{mass of Sun}\\ &= 2\times 10^{30} kg\\ m_{\rm j} &= \textrm{mass of Jupiter}\\ &= 1.90\times 10^{27} kg \end{align*}
Therefore: \begin{equation*} \mu=\frac{m_{\rm j}m_{\rm s}}{ m_{\rm j}+m_{\rm s}}=1.898\times 10^{27}kg\approx m_{\rm j}=.95\times 10^{-3}m_{\rm s} \end{equation*} and: \begin{align*} |{\vec r}_{\rm s}-{\vec r}_{\rm cm}| &= \left\vert{\vec r}_{\rm s}- \frac{m_{\rm j}{\vec r}_{\rm j} + m_{\rm s}{\vec r}_{\rm s}}{ m_{\rm j} + m_{\rm s}}\right\vert\\ &= \frac{m_{\rm j}}{m_{\rm j} + m_{\rm s}}|{\vec r}_{\rm s}-{\vec r}_{\rm j}|\\ &= 7.38\times 10^8m \end{align*}
Comparisons: \begin{align*} \frac{|{\vec r}_{\rm s}-{\vec r}_{\rm cm}|}{ R_{\rm s}} &= 1.05\\ \frac{|{\vec r}_{\rm s}-{\vec r}_{\rm cm}|}{|{\vec r}_{\rm s}-{\vec r}_{\rm j}|} &= 9.5\times 10^{-4} \end{align*} i.e. The center-of-mass, about which the Sun and Jupiter both rotate, is actually (just) outside the Sun itself!
-
Find \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) and \(\mu\) for the
Sun-Earth system. Compare \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) to
the radius of the Sun and to the distance from the Sun to the Earth.
Compare \(\mu\) to the mass of the Sun and the mass of the Earth.
- Undo Formulas for Center of Mass (Geometry)
S1 5238S
(Sketch limiting cases) Purpose: For two central force systems that share the same reduced mass system, discover how the motions of the original systems are the same and different.
The figure below shows the position vector \(\vec r\) and the orbit of a “fictitious” reduced mass \(\mu\).
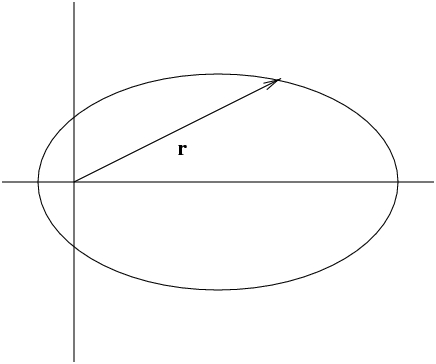
- Suppose \(m_1=m_2\), Sketch the position vectors and orbits for \(m_1\) and \(m_2\) corresponding to \(\vec{r}\). Describe a common physics example of central force motion for which \(m_1=m_2\).
Our final answer should be a sketch of two orbits (one for each mass) with labeled position vectors.
Because \({\vec r}={\vec r}_2-{\vec r}_1=\left(1 + {m_2\over m_1}\right)\, {\vec r}_2 =2\, {\vec r}_2\), we have
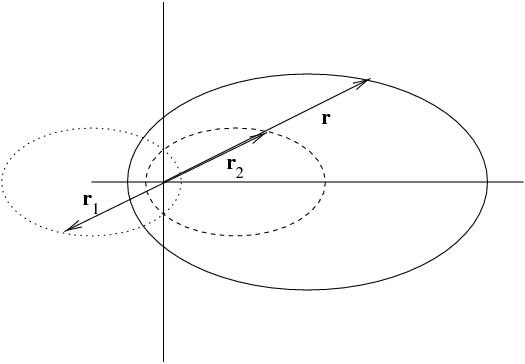
Notice that \(|{\vec r}|=|{\vec r}_1|+|{\vec r}_2|\) and that the orbits are reflections of each other through the origin. A common physics example would be motion of equal mass binary stars. A particle physics example would be positronium.
- Repeat, for \(m_2>m_1\).
In this case we have \({\vec r}={\vec r}_2-{\vec r}_1=\left(1 + {m_2\over m_1}\right)\, {\vec r}_2 =\alpha\, {\vec r}_2\), where \(\alpha>2\). The example I have plotted below is for \(\alpha={4}\), i.e. \(m_2=3m_1\). We have
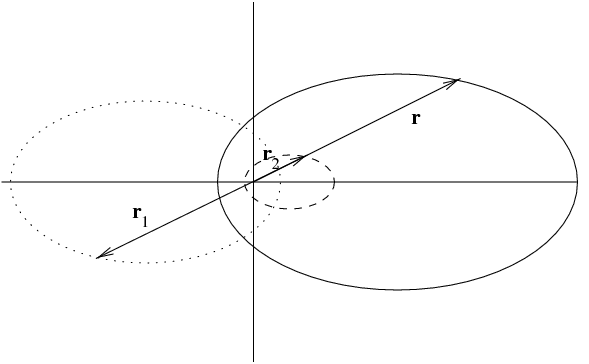
Notice that even for this relatively small value of \(\alpha\) that the orbit of \(m_2\) is closer to lying inside the orbit of \(m_1\). An interesting challenge question is: What is the smallest value of \(\alpha\) for which one orbit lies entirely inside the other?
A common physics example of \(m_2>m_1\) would be a neutron star rotating around a black hole or a planet rotating around a star.
- Suppose \(m_1=m_2\), Sketch the position vectors and orbits for \(m_1\) and \(m_2\) corresponding to \(\vec{r}\). Describe a common physics example of central force motion for which \(m_1=m_2\).
- Angular Momentum and Kinetic Energy in the Center of Mass
S1 5238S
(Messy algebra) Convince yourself that the expressions for kinetic energy in original and center of mass coordinates are equivalent. The same for angular momentum.
Consider a system of two particles of mass \(m_1\) and \(m_2\).
-
Show that the total kinetic energy of the system is the same as that of two
“fictitious” particles: one of mass \(M=m_1+m_2\) moving with the velocity of the
center of mass and one of mass \(\mu\) (the reduced mass) moving with the
velocity of the relative position.
In this problem, you are trying to show that the total kinetic energy of the system of two particles \(m_1\) and \(m_2\) is the same as the total kinetic energy of the two “fictitious” particles: \begin{equation*} T_{total}=\frac{1}{2}m_1\vert\dot{\vec{r}}_1\vert^2 +\frac{1}{2}m_2\vert\dot{\vec{r}}_2\vert^2 =\frac{1}{2}M\vert\dot{\vec{R}}\vert^2 +\frac{1}{2}\mu\vert\dot{\vec{r}}\vert^2 \end{equation*}
In the calculation below, make sure that you used the vector square, i.e. for any vector \(\vec{a}\) the square of the norm \(\vert \vec{a}\vert^2\) is given by the dot product of the vector with itself: \begin{equation*} \vert \vec{a}\vert^2=\vec{a}\cdot\vec{a} \end{equation*}
You can start from either side of this equation and show that it is equal to the other side - here I will start from the left. The center of mass position is \(\vec{R}=\frac{m_1}{M}\vec{r_1}+\frac{m_2}{M}\vec{r_2}\) and the relative position is \(\vec{r}=\vec{r_2}-\vec{r_1}\). \begin{align*} \vec{r}_2 &= \vec{r}+\vec{r}_1 \\ \Longrightarrow\vec{R} &= \frac{m_1}{M}\vec{r_1}+\frac{m_2}{M} \left(\vec{r}+\vec{r}_1\right)\\ &=\frac{m_2}{M}\vec{r}+\frac{m_1+m_2}{M}\vec{r}_1 \\ &=\frac{m_2}{M}\vec{r}+\vec{r}_1 \\ \Longrightarrow \vec{r}_1&=\vec{R}-\frac{m_2}{M}\vec{r} \\ \textrm{Likewise: } \vec{r}_2 &=\vec{R}+\frac{m_1}{M}\vec{r} \end{align*} Using these relationships: \begin{align*} T &= \frac{1}{2}m_1 v_1^2+\frac{1}{2}m_2 v_2^2\\ &= \frac{1}{2}m_1\vert\dot{\vec{r}}_1\vert^2 +\frac{1}{2}m_2\vert\dot{\vec{r}}_2\vert^2\\ &=\frac{1}{2}m_1\left|\dot{\vec{R}}-\frac{m_2}{M}\dot{\vec{r}}\right|^2 +\frac{1}{2}m_2\left|\dot{\vec{R}}+\frac{m_1}{M}\dot{\vec{r}}\right|^2\\ &=\frac{1}{2}m_1\left(\dot{\vec{R}}^2 -\frac{2 m_2}{M}\dot{\vec{R}}\cdot\dot{\vec{r}} +\frac{m_2^2}{M^2}\dot{\vec{r}}^2\right) +\frac{1}{2}m_2\left(\dot{\vec{R}}^2 +\frac{2 m_1}{M}\dot{\vec{R}}\cdot\dot{\vec{r}} +\frac{m_1^2}{M^2}\dot{\vec{r}}^2\right)\\ &=\frac{1}{2}\left(m_1+m_2\right)\dot{\vec{R}}^2 +\frac{1}{2} \frac{m_1m_2\left(m_1+m_2\right)}{M^2}\dot{\vec{r}}^2 \quad \textrm{ (cross terms cancel)}\\ &=\frac{1}{2}M\dot{\vec{R}}^2 +\frac{1}{2}\frac{m_1m_2}{m_1+m_2}\dot{\vec{r}}^2\\ &=\frac{1}{2}M\dot{\vec{R}}^2 +\frac{1}{2}\mu\dot{\vec{r}}^2 \end{align*} where \(M\) is the total mass, \(\dot{\vec{R}}\) is the center of mass velocity, \(\mu\) is the reduced mass, and \(\dot{\vec{r}}\) is the relative velocity.
-
Show that the total angular momentum of the system can similarly be decomposed
into the angular momenta of these two fictitious particles.
For this part, you are trying to show that the total angular momentum of the system of two particles \(m_1\) and \(m_2\) is the same as the total angular momentum of the system of two “fictitious” particles. \begin{align*} \vec{L} &= \vec{r}_1\times\vec{p}_1+\vec{r}_2\times\vec{p}_2\\ &=\vec{r}_1\times m_1\dot{\vec{r}}_1 +\vec{r}_2\times m_2\dot{\vec{r}}_2\\ &=\vec{R}\times M\dot{\vec{R}}+\vec{r}\times \mu\dot{\vec{r}} \end{align*}
In the calculation below, notice the allowed algebraic manipulations with the cross product. Like other forms of “multiplication,” the cross product is linear, i.e. you are allowed to FOIL.
Using the same relationships found in part (a) between \(\vec{r}_1\), \(\vec{r}_2\), \(\vec{R}\), \(\vec{r}\), we have: \begin{align*} \vec{L} &= \vec{r}_1\times\vec{p}_1+\vec{r}_2\times\vec{p}_2\\ &=\vec{r}_1\times m_1\dot{\vec{r}}_1 +\vec{r}_2\times m_2\dot{\vec{r}}_2\\ &=\left(\vec{R}-\frac{m_2}{M}\vec{r}\right)\times m_1\left(\dot{\vec{R}} -\frac{m_2}{M}\dot{\vec{r}}\right) +\left(\vec{R}+\frac{m_1}{M}\vec{r}\right)\times m_2\left(\dot{\vec{R}} +\frac{m_1}{M}\dot{\vec{r}}\right)\\ &= m_1\vec{R}\times\dot{\vec{R}} -\frac{m_1 m_2}{M}\vec{r}\times\dot{\vec{R}} -\frac{m_1 m_2}{M}\vec{R}\times\dot{\vec{r}} +\frac{m_1 m_2^2}{M^2}\vec{r}\times\dot{\vec{r}}\\ & m_2\vec{R}\times\dot{\vec{R}} +\frac{m_1 m_2}{M}\vec{r}\times\dot{\vec{R}} +\frac{m_1 m_2}{M}\vec{R}\times\dot{\vec{r}} +\frac{m_1^2 m_2}{M^2}\vec{r}\times\dot{\vec{r}}\\ &=\left(m_1+m_2\right) \vec{R}\times\dot{\vec{R}} +\frac{m_1 m_2\left(m_1+m_2\right)}{M^2} \vec{r}\times\dot{\vec{r}}\\ &=\vec{R}\times M\dot{\vec{R}}+\vec{r}\times \mu\dot{\vec{r}}\\ &=\vec{R}\times\vec{P}_{CM}+\vec{r}\times \vec{p}_{rel} \quad \left(\textrm{where } \vec{P}_{CM}=M\dot{\vec{R}} \textrm{ and } \vec{p}_{rel} =\mu\dot{\vec{r}}\right) \end{align*}
-
Show that the total kinetic energy of the system is the same as that of two
“fictitious” particles: one of mass \(M=m_1+m_2\) moving with the velocity of the
center of mass and one of mass \(\mu\) (the reduced mass) moving with the
velocity of the relative position.
- Confidence Rating
S1 5238S
After solving each problem on the assignment, indicate your answers to the following questions for each problem. Answer for the problem as a whole, even if the problem has multiple parts.
- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?

For the rest of the questions, assume you have interpreted the problem correctly - Problem Confidence How confident are you that you could independently come up with a correct solution process to a similar problem on a future problem set?

- Answer Confidence How confident are you that your final answer to this question is correct (not solution process)?

- Makes Sense To what degree do you understand how your answer fits (or does not fit) the physical or mathematical situation of the problem?

- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?