Central Forces: Spring-2025
HW 06 : Due W3 D5
- Scattering
S0 5242S
Consider a very light particle of mass \(\mu\) scattering from a very heavy, stationary particle of mass \(M\). The force between the two particles is a repulsive Coulomb force \(\frac{k}{r^2}\) (neglect the gravitational force). The impact parameter \(b\) in a scattering problem is defined to be the distance which would be the closest approach if there were no interaction (See Figure). The initial velocity (far from the scattering event) of the mass \(\mu\) is \(\vec v_0\).
Answer the following questions about this situation in terms of \(k\), \(M\), \(\mu\), \(\vec v_0\), and \(b\). (It is not necessarily wise to answer these questions in order.)
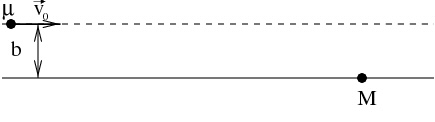
- What is the initial angular momentum of the system?
- What is the initial total energy of the system?
- What is the distance of closest approach \(r_{\rm{min}}\) with the interaction?
- Sketch the effective potential.
- What is the angular momentum at \(r_{\rm{min}}\)?
- What is the total energy of the system at \(r_{\rm{min}}\)?
- What is the radial component of the velocity at \(r_{\rm{min}}\)?
- What is the tangential component of the velocity at \(r_{\rm{min}}\)?
- What is the value of the effective potential at \(r_{\rm{min}}\)?
- For what values of the initial total energy are there bound orbits?
- Using your results above, write a short essay describing this type of scattering problem, at a level appropriate to share with another Paradigm student.
- Effective Potential Diagrams, version 2
S0 5242S
Consider a mass \(\mu\) in the potential shown in the graph below.
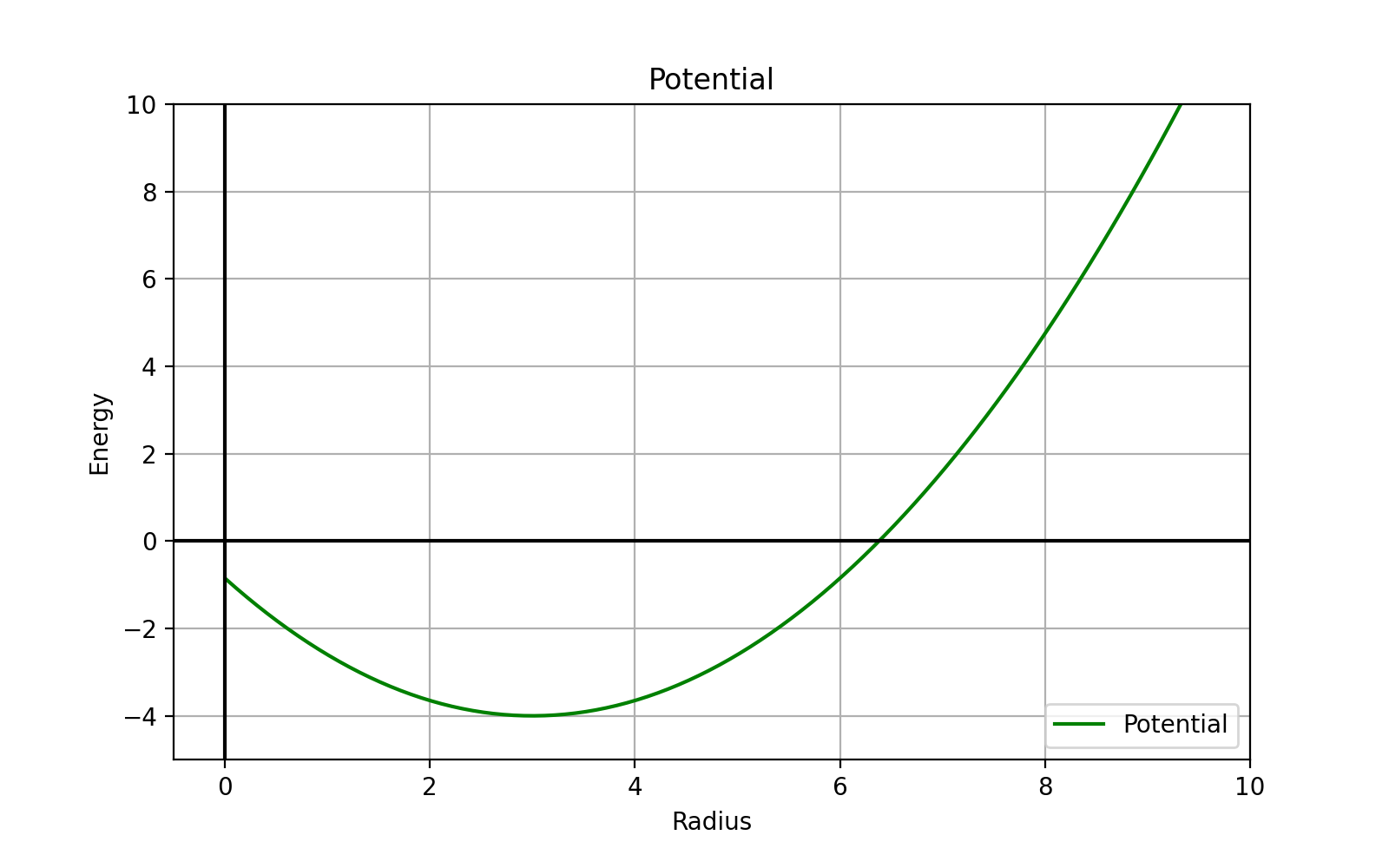
- Sketch the effective potential if the angular momentum is not zero.
- Describe qualitatively, the shapes of all possible types of orbits, indicating the energy for each in your diagram.
- Working with Representations on the Ring
S0 5242S
The following are 3 different representations for the \(\textbf{same}\) state on a quantum ring for \(r_0=1\) \begin{equation} \left|{\Phi_a}\right\rangle = i\sqrt{\frac{ 2}{12}}\left|{3}\right\rangle - \sqrt{\frac{ 1}{12}}\left|{1}\right\rangle +\sqrt{\frac{ 3}{12}}e^{i\frac{\pi}{4}}\left|{0}\right\rangle -i\sqrt{\frac{ 2}{ 12}}\left|{-1}\right\rangle +\sqrt{\frac{ 4}{12}}\left|{-3}\right\rangle \end{equation} \begin{equation} \left| \Phi_b\right\rangle \doteq \left( \begin{matrix} \vdots \\ i\sqrt{\frac{ 2}{12}}\\ 0 \\ -\sqrt{\frac{ 1}{12}} \\ \sqrt{\frac{ 3}{12}}e^{i\frac{\pi}{4}} \\ -i\sqrt{\frac{ 2}{12}}\\ 0 \\ \sqrt{\frac{4}{12} }\\ \vdots \end{matrix}\right) \begin{matrix} \leftarrow m=0 \end{matrix} \end{equation} \begin{equation} \Phi_c(\phi) \doteq \sqrt{\frac{1}{24 \pi}} \left( i\sqrt{2}e^{i 3 \phi} -e^{i\phi} +\sqrt{3}e^{i\frac{\pi}{4}} -i \sqrt{2} e^{-i\phi} + \sqrt{4}e^{-i 3 \phi} \right) \end{equation}
- With each representation of the state given above, explicitly calculate the probability that \(L_z=-1\hbar\). Then, calculate all other non-zero probabilities for values of \(L_z\) with a method/representation of your choice.
- Explain how you could be sure you calculated all of the non-zero probabilities.
- If you measured the \(z\)-component of angular momentum to be \(3\hbar\), what would the state of the particle be immediately after the measurement is made?
- With each representation of the state given above, explicitly calculate the probability that \(E=\frac{9}{2}\frac{\hbar^2}{I}\). Then, calculate all other non-zero probabilities for values of \(E\) with a method of your choice.
If you measured the energy of the state to be \(\frac{9}{2}\frac{\hbar^2}{I}\), what would the state of the particle be immediately after the measurement is made?
- Confidence Rating
S0 5242S
After solving each problem on the assignment, indicate your answers to the following questions for each problem. Answer for the problem as a whole, even if the problem has multiple parts.
- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?

For the rest of the questions, assume you have interpreted the problem correctly - Problem Confidence How confident are you that you could independently come up with a correct solution process to a similar problem on a future problem set?

- Answer Confidence How confident are you that your final answer to this question is correct (not solution process)?

- Makes Sense To what degree do you understand how your answer fits (or does not fit) the physical or mathematical situation of the problem?

- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?