Quantum Fundamentals: Winter-2026
HW 5 (SOLUTION): Due W3 D3
- Chained Stern-Gerlach (Brief)
S1 5419S
Consider the Stern-Gerlach set-up shown, with a thermal oven source, and some state vectors associated with various analyzer outputs:
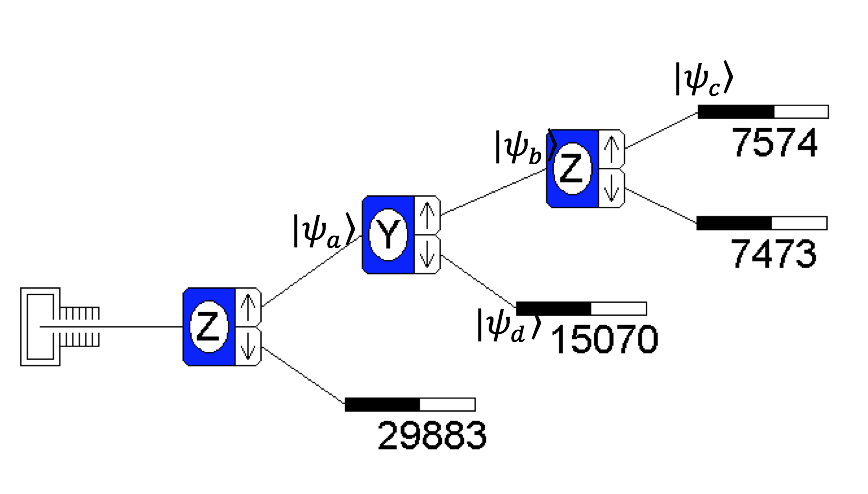
How many particles were released from the oven?
We can just add up all the particles from all the counters:
29883+15070+7473+7574 = 60000
Write down Dirac notation expressions for \(|\Psi_a\rangle\), \(|\Psi_b\rangle\), \(|\Psi_c\rangle\), and \(|\Psi_d\rangle\) in the \(S_z\) basis (i.e., as linear superpositions of \(|+\rangle_z\) and \(|-\rangle_z\)).
\(|\Psi_a\rangle = |+\rangle\)
\(|\Psi_b\rangle = \frac{1}{\sqrt{2}}|+\rangle+\frac{i}{\sqrt{2}}|-\rangle\)
\(|\Psi_c\rangle = |+\rangle\)
\(|\Psi_d\rangle = \frac{1}{\sqrt{2}}|+\rangle-\frac{i}{\sqrt{2}}|-\rangle\)
- Spin One Half Unknowns (Brief)
S1 5419S
Using the SPINS simulation for a spin-\(\tfrac{1}{2}\) system
(Spins simulation),
for the unknown initial state \(\left|{\psi_4}\right\rangle \), perform measurements of
\(S_x\), \(S_y\), and \(S_z\) separately, and for each measurement determine the probability of obtaining each possible measurement value.(We carried out the same procedure for \(\left|{\psi_3}\right\rangle \) in class; you may
refer to that example.)
- Use the probabilities you observed from the measurements to express \(\left|{\psi_4}\right\rangle \) as a linear superposition of the \(S_z\)-basis states \(\left|{+}\right\rangle \) and \(\left|{-}\right\rangle \).
You have experimentally obtained the relative probabilities with which the eigenvalues of operators \(\,\widehat{\!S}_z\), \(\,\widehat{\!S}_x\), and \(\,\widehat{\!S}_z\) show up, in measurements on the system in the unknown initial states \(\left|{\psi_i}\right\rangle \) (\(i=3,4\)). To find what the initial states were, expressed in the eigenbasis of the \(\,\widehat{\!S}_z\) operator, \(\{\left|{+}\right\rangle ,\left|{-}\right\rangle \}\), we use a general form for a quantum--mechanical state, \[ \left|{\psi_i}\right\rangle = a_i \left|{+}\right\rangle + b_i e^{i \phi_i} \left|{-}\right\rangle . \] where \(a_i\) and \(b_i\) are real and positive and \(\gamma_i\) is an angle. Notice that I can use the freedom in the overall phase for the state to make the coefficient on \(\left|{+}\right\rangle \) real and positive. If I were to use also set the phase of the coefficient of \(\left|{-}\right\rangle \) to be zero, i.e. if I simply chose \(\left|{\psi_i}\right\rangle = A_i \left|{+}\right\rangle + B_i \left|{-}\right\rangle \) I might not be able to write some states, since probabilities in measurements do depend on the relative phase in a state. (See one of the previous homework problems.)
Here, I will show how to find \(\left|{\psi_4}\right\rangle \), since it is the hardest case and then make some general comments.
The experimental results for the probabilities are, \begin{align*} & {P}(S_z = +\hbar/2) &= \frac{1}{4} \quad & {P}(S_z = -\hbar/2) &= \frac{3}{4} \\[6pt] & {P}(S_x=+\hbar/2) &= \frac{1}{2} \quad & {P}(S_x=-\hbar/2) &= \frac{1}{2} \\[6pt] & {P}(S_y=+\hbar/2) &= \frac{93}{100} \quad & {P}(S_y = -\hbar/2) &= \frac{7}{100} \end{align*}
Since I want to write \(\left|{\psi_4}\right\rangle \) in the \(\,\widehat{\!S}_z\) basis, I'll use those results first. \begin{align*} \mathcal{P}(S_z = +\hbar/2) &= \left|\left\langle {+}\middle|{\psi_4}\right\rangle \right|^2 \\ &= \left| \left\langle {+}\right| \Big( a_4 \left|{+}\right\rangle + b_4 e^{i\phi_4} \left|{-}\right\rangle \Big) \right|^2 \\ &= \frac{1}{4}\\ &\Rightarrow \ \left|a_4\right|^2 = \left(a_4\right)^2 = \frac{1}{4}, \\ a_4 &= \frac{1}{2} \\[6pt] \mathcal{P}(S_z = +\hbar/2) &= \left|\left\langle {-}\middle|{\psi_4}\right\rangle \right|^2 \\ &= \left| \left\langle {-}\right| \Big( a_4 \left|{+}\right\rangle + b_4 e^{i\phi_4} \left|{-}\right\rangle \Big) \right|^2\\ &= \frac{3}{4}\\ &\Rightarrow \ \left|b_4 e^{i\phi_4} \right|^2 = \left( b_4 \right)^2 = \frac{3}{4} \\ b_4 &= \frac{\sqrt{3}}{2} \end{align*}
did not get any information about \(\phi_4\).
Now use results of \(\,\widehat{\!S}_{x}\) and \(\,\widehat{\!S}_{y}\). Recall that I am working in the \(\,\widehat{\!S}_z\) basis, so I use expressions for \(\left|{\pm}\right\rangle _{x}\) and \(\left|{\pm}\right\rangle _{y}\) in that basis. \begin{align*} & \mathcal{P}(S_x = +\hbar/2) = \left|{}_x\left\langle {+}\middle|{\psi_4}\right\rangle \right|^2\\ &= \left| \frac{1}{\sqrt{2}} \Big( \left\langle {+}\right| + \left\langle {-}\right| \Big) \Big( \frac{1}{2} \left|{+}\right\rangle + \frac{\sqrt{3}}{2} e^{i\phi_4} \left|{-}\right\rangle \Big) \right|^2 \\ &= \frac{1}{2} \\ \rightarrow \frac{1}{2} &= \ \left| \frac{1}{2\sqrt{2}} + \frac{\sqrt{3}}{2\sqrt{2}} e^{i\phi_4} \right|^2 \\ &= \left( \frac{1}{2\sqrt{2}} + \frac{\sqrt{3}}{2\sqrt{2}} e^{-i\phi_4} \right) \left( \frac{1}{2\sqrt{2}} + \frac{\sqrt{3}}{2\sqrt{2}} e^{i\phi_4} \right) \\ &= \frac{1}{8} \Big( 1 + 3 + \sqrt{3} \left( e^{i\phi_4} + e^{-i\phi_4} \right) \Big)\\ &= \frac{1}{4} \Big( 2 + \sqrt{3}\, \cos\phi_4 \Big), \\ &\rightarrow \cos\phi_4 =0. \end{align*}
This yields two possible solutions: \(\phi_4 =\pm \, \pi/2\).
To distinguish between these two possible angles, I need to calculate yet another probability. (Note that using \(\left|{-}\right\rangle _x\) will give us the same result as above. Why? Because the two probabilities contain the same information - if you know one, you know both.)
I'll use a result of measurement of \(\,\widehat{\!S}_y\). \begin{align*} \mathcal{P}(S_y = +\hbar/2) &= \left|{}_y\left\langle {+}\middle|{\psi_4}\right\rangle \right|^2\\ &= \left| \frac{1}{\sqrt{2}} \Big( \left\langle {+}\right| - i \left\langle {-}\right| \Big) \Big( \frac{1}{2} \left|{+}\right\rangle + \frac{\sqrt{3}}{2} e^{i\phi_4} \left|{-}\right\rangle \Big) \right|^2 \\ &= 0.93 \\ 0.93 &= \left| \frac{1}{2\sqrt{2}} - i \frac{\sqrt{3}}{2\sqrt{2}} e^{i\phi_4} \right|^2 \\ &= \left( \frac{1}{2\sqrt{2}} - i \frac{\sqrt{3}}{2\sqrt{2}} e^{i\phi_4} \right) \left( \frac{1}{2\sqrt{2}} + i \frac{\sqrt{3}}{2\sqrt{2}} e^{-i\phi_4} \right) \\ &= \frac{1}{8} \Big( 4 + i \sqrt{3}\, \Big( \underbrace{ e^{-i\phi_4} - e^{i\phi_4} }_{ = \, -2\,i\,\sin\,\phi_4 } \Big) \Big) \\ &= \frac{1}{4} \Big( 2 + \sqrt{3}\sin\phi_4 \Big) \\ &\rightarrow \sin\phi_4 \approx 1. \end{align*}
This is too close to \(1\) to resist. So this result says that \(\theta_4 = \frac{\pi}{2}\). This agrees with the previous calculation \(\cos(\pi/2)=0\). Thus we have found that the unknown state is:
\[ \left|{\psi_4}\right\rangle = \frac{1}{2}\left|{+}\right\rangle + \frac{\sqrt{3}}{2}\, e^{i \frac{\pi}{2}} \left|{-}\right\rangle \Big) \]
To find \(\left|{\psi_3}\right\rangle \) one runs through much the same procedure. \begin{eqnarray*} \left|{\psi_3}\right\rangle &=&\frac{1}{\sqrt{3}}\left|{+}\right\rangle +\frac{\sqrt{2}}{\sqrt{3}}e^{i\frac{\pi}{2}}\left|{-}\right\rangle \end{eqnarray*}
- Articulate a Process: Write a set of general instructions that would allow another student in next year's class to find an unknown state from probabilities obtained from spin
measurements.
- Represent the unknown state with its phase factor, as \(\left|{\psi}\right\rangle = a\left|{+}\right\rangle + b e^{i\gamma}\left|{-}\right\rangle \).
- Calculate the unknowns \(a\) and \(b\) by projecting onto the \(z\)-basis. \begin{eqnarray*} \left\langle {+}\middle|{\psi}\right\rangle &=a \\ \left\langle {-}\middle|{\psi}\right\rangle &=b \\ \end{eqnarray*}
- Compare these equations to the probabilities from the experiment (which are the squares of the norms of these equations) and thereby identify \(a\) and \(b\).
- Project the unknown state \(\left|{\psi}\right\rangle \) onto the the bra \(\left\langle {+}\right|_{x}\) and compare to the probabilities from the experiment. This will give one equation for the unknown angle \(\gamma\).
- If there is still an ambiguity that says \(\gamma\) is one of two possible angles, repeat the step above by projecting onto the bra \(\left\langle {+}\right|_{y}\), which will give a second equation for the unknown angle \(\gamma\) which will remove the ambiguity.
- Compare Theory with Experiment: Design an experiment that will
allow you to test whether the state you identified in Question (a) for the
unknown state \(\left|{\psi_4}\right\rangle \) is correct. Describe your experiment here, clearly but succinctly, as if you were writing it up for a paper. Do the experiment and discuss your results.
From the spin reference sheet, we see that the spin-1/2 state which is pure spin up according to a Stern-Gerlach device oriented in the \(\hat{n}\) direction is given in the \(z\)-basis by: \[\left|{+}\right\rangle _n =\cos{\frac{\theta}{2}}\left|{+}\right\rangle + \sin{\frac{\theta}{2}}\, e^{i\phi}\, \left|{-}\right\rangle \] where \(\theta\) and \(\phi\) are the angles that describe the orientation of the Stern-Gerlach device in spherical coordinates. By comparing this expression to our expression for the unknown state, I infer the direction for which the unknown state is “spin up”. By running the unknown state through a Stern-Gerlach device in this orientation, we should get all of the particles coming out the “up” port with 100% probability.
- Make a Conceptual Connection: In general, are the probabilities
obtained from spin-component measurements along only two spin directions (for example, the \(z\) direction and the \(y\) direction) sufficient to determine a spin-\(\tfrac{1}{2}\) quantum state? Why or why not?
No, in general, you need there are three unknowns, so you need three independent pieces of information to solve for them. The probabilities for two component-directions is only two pieces of independent information.
- Use the probabilities you observed from the measurements to express \(\left|{\psi_4}\right\rangle \) as a linear superposition of the \(S_z\)-basis states \(\left|{+}\right\rangle \) and \(\left|{-}\right\rangle \).
- Spin Calculations (brief)
S1 5419S
A set of spin-1/2 particles are identically prepared in the state \[\left|{\psi_A}\right\rangle =N\bigg(\sqrt{3}\left|{+}\right\rangle +e^{i\pi/3}\left|{-}\right\rangle \bigg)\] .
Determine \(N\) so that the state is normalized.
\begin{align*} 1 &= \left\langle {\psi_A}\middle|{\psi_A}\right\rangle \\ &= |N|^2 \bigg(\sqrt{3}\left\langle {+}\right|+e^{i\pi/3}\left\langle {-}\right|\bigg)\bigg(\sqrt{3}\left|{+}\right\rangle +e^{i\pi/3}\left|{-}\right\rangle \bigg)\\ &= |N|^2 \bigg(3 + 1\bigg)\\ \rightarrow N &= \frac{1}{2} \end{align*}
What values of the z-component of spin might you measure and with what probabilities?
Values are \(\pm \frac{\hbar}{2}\).
\begin{align*} \mathcal{P}(S_z = \hbar/2) &= |\left\langle {+}\middle|{\psi_A}\right\rangle |^2\\ &= \frac{3}{4} \\ \mathcal{P}(S_z = -\hbar/2) &= |\left\langle {+}\middle|{\psi_A}\right\rangle |^2\\ &= \frac{1}{4} \\ \end{align*}
What values of the y-component of spin might you measure and with what probabilities?
Values are \(\pm \frac{\hbar}{2}\).
\begin{align*} \mathcal{P}(S_y = \hbar/2) &= |\,{}_y\left\langle {+}\middle|{\psi_A}\right\rangle |^2\\ &=| \Big(\frac{1}{\sqrt{2}}\left\langle {+}\right| -\frac{i}{\sqrt{2}}\left\langle {-}\right| \Big) \bigg(\frac{\sqrt{3}}{2}\left|{+}\right\rangle +\frac{e^{i\pi/3}}{2}\left|{-}\right\rangle \bigg)|^2\\ &= | \Big(\frac{1}{\sqrt{2}}\frac{\sqrt{3}}{2} -\frac{i}{\sqrt{2}}\frac{e^{i\pi/3}}{2} \Big)|^2\\ &= \frac{1}{8} | \sqrt{3}-ie^{i\pi/3}|^2\\ &= \frac{1}{8} ( \sqrt{3}-ie^{i\pi/3})( \sqrt{3}+ie^{-i\pi/3})\\ &= \frac{1}{8} (3+1 -i\sqrt{3}e^{i\pi/3} + i\sqrt{3}e^{-i\pi/3}) \\ &= \frac{1}{8} (3+1 -i\sqrt{3}(e^{i\pi/3} - e^{-i\pi/3})) \\ &= \frac{1}{8} (4 -i\sqrt{3}(2i\sin\frac{\pi}{3})) \\ &= \frac{1}{2} + \frac{2}{8}\sqrt{3} \frac{\sqrt{3}}{2} \\ &= \frac{7}{8}\\ \mathcal{P}(S_y = -\hbar/2) &= |\,{}_y\left\langle {+}\middle|{\psi_A}\right\rangle |^2\\ &= 1-\mathcal{P}(S_y = \hbar/2)\\ &= \frac{1}{8} \\ \end{align*}
Write this state in the \(S_x\) basis (i.e., as a linear superposition of \(|+\rangle_x\) and \(|-\rangle_x\)).
\begin{align*} I\left|{\psi_A}\right\rangle &= \Big(\left|{+}\right\rangle _x {}_x\left\langle {+}\right| + \left|{-}\right\rangle _x {}_x\left\langle {-}\right| \Big) \bigg(\frac{\sqrt{3}}{2}\left|{+}\right\rangle +\frac{e^{i\pi/3}}{2}\left|{-}\right\rangle \bigg)\\ &= \bigg(\left|{+}\right\rangle _x {}_x\left\langle {+}\right|\frac{\sqrt{3}}{2}\left|{+}\right\rangle + \left|{+}\right\rangle _x {}_x\left\langle {+}\right|\frac{e^{i\pi/3}}{2}\left|{-}\right\rangle \\ & + \left|{-}\right\rangle _x {}_x\left\langle {-}\right|\frac{\sqrt{3}}{2}\left|{+}\right\rangle + \left|{-}\right\rangle _x {}_x\left\langle {-}\right|\frac{e^{i\pi/3}}{2}\left|{-}\right\rangle \bigg)\\ &= \frac{\sqrt{3}}{2}\frac{1}{\sqrt{2}}\left|{+}\right\rangle _x + \frac{e^{i\pi/3}}{2}\frac{1}{\sqrt{2}}\left|{+}\right\rangle _x \\ & + \frac{\sqrt{3}}{2}\frac{1}{\sqrt{2}}\left|{-}\right\rangle _x + \frac{e^{i\pi/3}}{2}\frac{-1}{\sqrt{2}}\left|{-}\right\rangle _x \\ &= \frac{\sqrt{3}+e^{i\pi/3}}{2\sqrt{2}}\left|{+}\right\rangle _x + \frac{\sqrt{3}-e^{i\pi/3}}{2\sqrt{2}}\left|{-}\right\rangle _x \end{align*}
In what direction would you have to orient a Stern-Gerlach analyzer so that ALL the particles prepared in the state \(\left|{\psi_A}\right\rangle \) would be measured to have a spin component in that direction equal to \(+\hbar/2\)? Give the direction in spherical coordinates, \(\theta\) and \(\phi\).
\begin{align*} \left\langle {+}\middle|{+}\right\rangle _n &= \left\langle {+}\middle|{\psi_A}\right\rangle \\ \cos \frac{\theta}{2} &= \frac{\sqrt{3}}{2} \\ \frac{\theta}{2} &= \frac{\pi}{6}\\ \theta &= \frac{\pi}{3}\\[12pt] \phi &= \frac{\pi}{3} \end{align*}