Quantum Fundamentals: NoTerm-2022
Complex Number Practice : Due Day 3 W 2/9 Math Bits

1. Complex Numbers: Rectangular Form S0 4362S For the complex numbers \(z_1=3-4i\) and \(z_2=7+2i\), compute:
   1. \(z_1-z_2\)
   2. \(z_1 \, z_2\)
   3. \(\frac{z_1}{z_2}\)
2. Circle Trigonometry and Complex Numbers S0 4362S

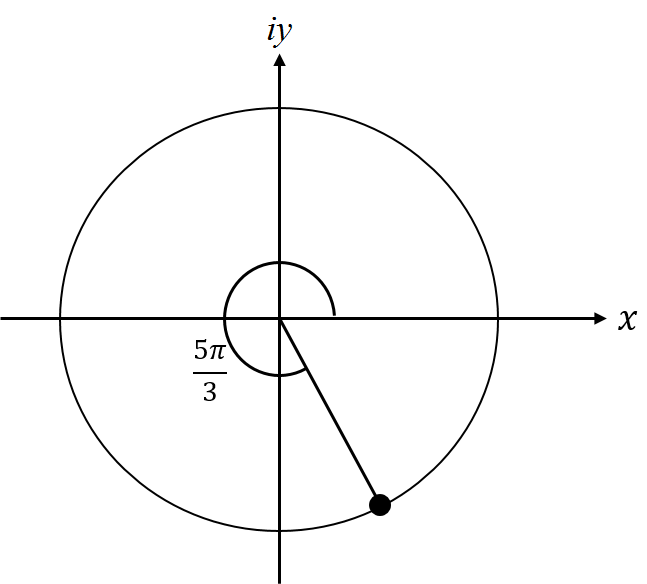
   Find the rectangular coordinates of the point where the angle \(\frac{5\pi}{3}\) meets the unit circle. If this were a point in the complex plane, what would be the rectangular and exponential forms of the complex number? (See figure.)

   

3. Complex Number Algebra, Exponential to Rectangular--Practice S0 4362S If \(z_1=5e^{7i\pi/4}\), \(z_2=3e^{-i\pi/2}\), and \(z_3=9e^{(1+i\pi)/3}\), express each of the following complex numbers in rectangular form, i.e. in the form \(x+iy\) where \(x\) and \(y\) are real.
   1. \( z_1 +z_2 \)
   2. \( z_1 z_2 \)
   3. \( \frac{z_2}{z_3} \)
4. Complex Numbers, All Forms--Practice S0 4362S Represent the following four complex numbers in rectangular form \(a + ib\), exponential form \(|z|e^{i\phi}\) , and on an Argand diagram:

   1. \(e^{i\pi}\)

   2. \(i\)

   3. \(\sin\frac{\pi}{2}\)

   4. \(\cos\frac{\pi}{4}-i\sin\frac{\pi}{4}\)