Oscillations and Waves: Spring-2025
HW 5a (SOLUTION): Due W5 D2

  1. Reflection and Transmission at a Sharp Boundary S1 5218S A traveling wave in a string is incident from the left (L) and propagates at speed \(v_1\), encountering a second string at \(x=0\). It partially reflects, returning in the same string with speed \(v_1\). It partially continues into a second string, traveling with speed \(v_2\). \begin{equation*} \psi(x,t)= \begin{cases} \psi_L(x,t)=Re[Ae^{i(-\omega_1 t+k_1 x)}]+Re[Be^{i(-\omega_1 t-k_1 x)}]\,&\text{ for }x\leq0\\ \psi_R(x,t)=Re[Ce^{i(-\omega_2 t+k_2 x)}] &\text{ for }x\geq0 \end{cases} \end{equation*}

    1. Explain the meanings of the terms in the wavefunctions and say which directions the waves propagate.

      • The first term describes a sinusoidal wave of amplitude \(A\) incident from the left and traveling right (in direction \(+x\); relative \(-\) sign between \(\omega\) and \(k\)) with velocity \(v_1=\frac{\omega}{k_1}\) and wavelength \(\lambda_1=\frac{2\pi}{k_1}\).
      • The second term describes a reflected wave of amplitude \(B\) traveling left (in direction \(-x\); relative \(+\) sign between \(\omega\) and \(k\)) with the same magnitude of \(\lambda_1=\frac{2\pi}{k_1}\).
      • These two add to make the total wave on the left.
      • The third term describes a transmitted wave of amplitude \(C\) traveling right (in direction \(+x\)) with velocity \(v_2=\frac{\omega}{k_2}\) and wavelength \(\lambda_2=\frac{2\pi}{k_2}\).

    2. Explain why \(\omega_1=\omega_2=\omega\)

      The continuity of the string at the boundary requires that the frequencies on both sides be the same. If they were different, a unique displacement could not be defined.

    3. What equation represents the statement, “The string must be continuous at the boundary”? Show that it leads to \(A+B=C\).

      The statement in (b) is necessary for continuity, but it is not sufficient. The boundary is at \(x=0\) and the rope is continuous at all times \(t\), so the displacement must be the same at this position whether we use the “left” or the “right” wave function.

      \(\psi_L(0,t)=\psi_R(0,t)\)

      Substitute: \(Re[Ae^{i(-\omega t+k_10)}]+Re[Be^{i(-\omega t-k_1 0)}]=Re[Ce^{i(-\omega t+k_2 0)}]\)

      Note the times cancel, so \(A+B=C\).

    4. Write the piecewise function for \(\frac{\partial\psi(x,t)}{\partial x}\).

      \begin{equation*} \frac{\partial\psi(x,t)}{\partial x}= \begin{cases} Re[-ik_1Ae^{i(-\omega_1 t+k_1 x)}]+ Re[ik_1Be^{i(-\omega_1 t-k_1 x)}]\,&\text{ for }x\leq0\\ Re[ik_2Ce^{i(-\omega_2 t+k_2 x)}] &\text{ for }x\geq0 \end{cases} \end{equation*}

    5. What equation represents the statement, “The transverse component of the force at the boundary must sum to zero”? Show that it leads to \(k_1A-k_1B=k_2C\)

      The boundary is at \(x = 0\) and the transverse component of the tension in the rope is: \(T\sin{\theta}\approx T\tan{\theta}\approx T\frac{\partial\psi}{\partial x}\). If the tension remains the same in both ropes, then the derivative is continuous at the boundary.

      \(\frac{\partial}{\partial x}\psi_L(0,t)=\frac{\partial}{\partial x}\psi_R(0,t)\)

      Substitute:

      \(Re[-ik_1Ae^{i(-\omega_1 t+k_1 x)}]+ Re[ik_1Be^{i(-\omega_1 t-k_1 x)}]=Re[ik_2Ce^{i(-\omega_2 t+k_2 x)}]\)

      Note the times cancel, as does \(i\), so:

      \(Ak_1-Bk_1=Ck_2\).

    6. Solve the equations in (c) and (e) and find the displacement reflection and transmission coefficients \(R_\psi\equiv\frac{B}{A}=\frac{k_1-k_2}{k_1+k_2}\) and \(T_\psi\equiv\frac{C}{A}=\frac{2k_1}{k_1+k_2}\).

      Take the ratio of the reflectd (left moving) to th incident (right moving) rope in the “left” medium, or medium \(1\), to define: \(R_\psi\equiv\frac{B}{A}\).

      Use:
      \(A+B=C; (1)\)

      \(Ak_1-Bk_1=Ck_2; (2)\)

      solve \((1)\) for \(C\) and substitute in \((2)\).

      \(Ak_1-Bk_1=(A+B)k_2\)

      \(Ak_1-Ak_2=Bk_2+Bk_1\)

      \(A(k_1-k_2)=B(k_2+k_1)\)

      \(R_\psi\equiv\frac{B}{A}=\frac{k_1-k_2}{k_1+k_2}\)

      Now substitute for \(B\) in \((1)\).

      \(A+A\frac{k_1-k_2}{k_1+k_2}=C\)

      \(A+(1+\frac{k_1-k_2}{k_1+k_2})=C\rightarrow A\Big(\frac{2k_1}{k_1+k_2}\big)=C\)

      Take the ratio of the height of the transmitted (right moving in medium \(2\)) to the incident (right moving in medium \(1\)) to define: \(T_\psi\equiv\frac{C}{A}=\frac{2k_1}{k_1+k_2}\)

    7. Look carefully at the expression in (d) and show that you can define a reflection coefficient for \(\frac{\partial\psi}{\partial x}\) and that it is \(R_{\frac{\partial\psi}{\partial x}}=\frac{k_2-k_1}{k_1+k_2}\)

      The equation in (d) is similar to the equation above (a) in that is has the same left- and right-moving waves, but just the amplitudes (coefficients) are different. So take the ratio of the height of the reflected (left moving) to the incident (right moving) move in the “left” medium, or medium \(1\) to define:

      \[R_{\partial\psi/\partial x}\equiv\frac{-ik_1 B}{ik_1 A}=-R_\psi=\frac{k_2-k_1}{k_2+k_1} \]

    8. Look carefully at the expression in (d) and show that you can define a transmission coefficient for \(\frac{\partial\psi}{\partial x}\) and that it is \(T_{\frac{\partial\psi}{\partial x}}=\frac{2k_2}{k_1+k_2}\)

      The equation in (d) is similar to the equation above (a) in that is has the same left- and right-moving waves, but just the amplitudes (coefficients) are different. Take the ratio of the height of the transmitted (right moving in medium \(2\)) to the incident (right moving in medium 1) to define

      \[R_{\partial\psi/\partial x}\equiv\frac{ik_2 C}{ik_1 A}=\frac{2k_2}{k_2+k_1}\]

      In class, we're going to show that the \(k\) values can be replaced by impedances, and it's the coefficients in (g) and (h) that you're measuring in Tuesday's lab.

  2. Light Propagation in a Vacuum S1 5218S Light propagates in vacuum with speed \(c\) and in a medium with speed \(v = \frac{c}{n}\) where \(n\) is the refractive index (\(n>1\)). (The refractive index is not an integer!) Show that when light is incident from vacuum (\(n=1\)) onto glass (\(n=1.5\)), about 4% of the energy (which is proportional to \(|\psi|^2\) is reflected. Also show that the light changes its phase angle by \(\pi\) when it is reflected.

    In medium \(1\), \(v_1=\frac{c}{n_1}=c\). In medium \(2\), \(v_2=\frac{c}{n_2}=\frac{c}{1.5}=\frac{2}{3}c\).

    In this case the reflected light amplitude is: \[R_\psi\equiv\frac{B}{A}=\frac{k_1-k_2}{k_1+k_2}=\frac{v_2-v_1}{v_2+v_1}=\frac{\frac{2}{3}c-c}{\frac{2}{3}c+c}=\frac{-\frac{1}{3}c}{\frac{5}{3}c}= -\frac{1}{5}=-0.2 \] The negative sign says the phase change is \(\pi\) (the wave is inverted).

    The square of the amplitude reflection coefficient, which gives the reflected energy is \(|0.2|^2 = 0.04 = 4\%\)

  3. Square Wave in a Rope S1 5218S A rectangular traveling pulse is launched with speed \(v_1\) from the left into a very long rope. At the boundary at \(x=0\), the pulse is partially reflected and partially transmitted into a second rope where the transmitted pulse moves with velocity \(v_2\). The reflected (black) and transmitted (red) pulses are depicted some time after the original pulse encounters the boundary. The system obeys the NDWE.

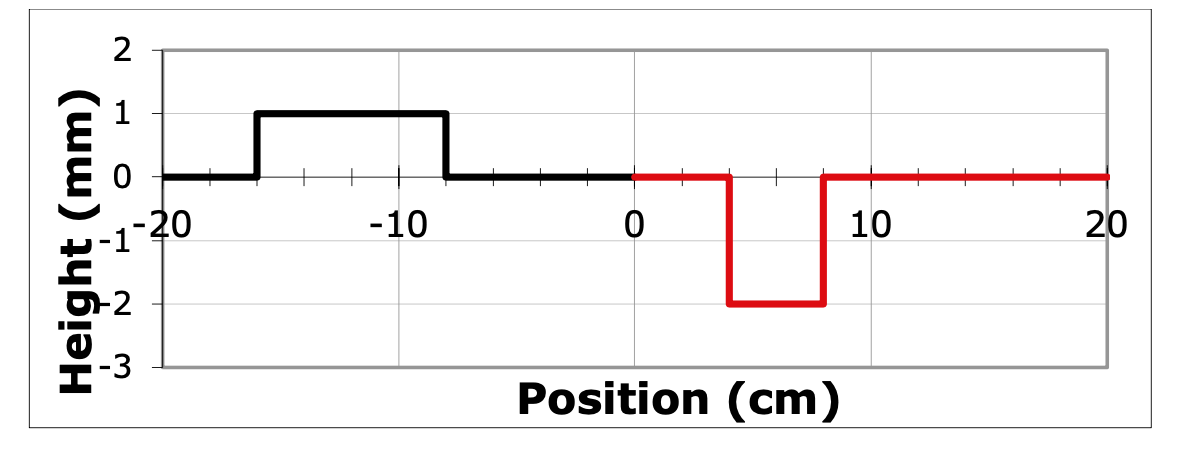    Figure: A point in time of the graph of a square wave after reflecting and transmitting at \(x=0\).

    1. Use the widths of the reflected and transmitted pulses to find the ratio of \(v_1\) to \(v_2\). Explain.

      The pulse in the red medium \((2)\) is shorter than the pulse in the black medium \((1)\) by a ratio of \(\frac{2}{4}=\frac{1}{2}\). Therefore, because the frequency is the same on both sides, and the velocity is related to the frequency and wavelength by \(\frac{v_2}{v_1}=\frac{f\lambda_2}{f\lambda_1}=\frac{\lambda_2}{\lambda_1}=\frac{1}{2}\)

    2. Calculate the relative velocities using the pulse locations and show that this is consistent with (a).

      The leading edge of each pulse tells how far the pulse has traveled since the incident pulse hit the boundary, a time we'll call \(\Delta t\). Therefore, if each distance is \(d_1\) or \(d_2\),

      \(\frac{v_2}{v_1}=\frac{d_2/\Delta t}{d_1/\Delta t}=\frac{d_2}{d_1}=\frac{4}{8}=\frac{1}{2}\)

    3. Is the mass density of the red rope smaller or larger than the black rope? Why?

      The transmitted wave is opposite in polarity to the reflected wave.

      That means \(\frac{T_\psi}{R_\psi}=\frac{2v_2}{v_2-v_1}<0\), which implies \(v_2<v_1\).

      Therefore, if \(v_2<v_1\), then \(\sqrt{\frac{T}{\mu_2}}<\sqrt{\frac{T}{\mu_1}}\text{ and } \mu_2>\mu_1\).

    4. Describe the original pulse (height, polarity, length), showing qualitative and quantitative reasoning.

      The original pulse must have the same width as the reflected pulse because it is in the same medium and all components keep the same wavelength on reflection.

      The reflection coefficient is negative, so the incident pulse is inverted. We could also note that transmitted pulses retain their polarity, so the incident must be inverted.

      Height of the incident pulse: \(R_\psi\equiv\frac{B}{A}=\frac{v_2-v_1}{v_2+v_1}=\frac{\frac{1}{2}v_1-v_1}{\frac{1}{2}v_1+v_1}=\frac{-\frac{1}{2}}{\frac{3}{2}}=-1/3\), so \(A=3B\) and the original pulse height is \(A=3\,mm\).

    5. Can you determine the velocities \(v_1\) and \(v_2\)? If so, what are they, and if not, what information would you need?

      No, we can only determine the ratio, as above. We would need the time since the boundary encounter to know the actual velocities. But we learned a lot!