Energy and Entropy: Fall-2024
HW 6 (updated 3:40pm Mon) (SOLUTION): Due Day 20 Tues 10/22

1. Analyze TS rectangle S1 5076S Consider a monatomic ideal gas that undergoes a 4-step cyclic process. On a \(T\)-\(S\) diagram, the four steps of the process trace out a rectangle. The cycle proceeds in the clockwise direction around the rectangular path. The four sides of the rectangle correspond to
   (A) Constant temperature, \(T_h\)
   (B) Constant entropy, \(S_h\)
   (C) Constant temperature, \(T_l\)
   (D) Constant entropy, \(S_l\)
   
   1. Make a \(T\)-\(S\) diagram that represents this cyclic process. Label the axes, the four steps (A through D), the direction of each process, and the key values of \(S\) and \(T\). The horizontal axis corresponds to which variable? Why?
   2. Does a clockwise path in \(T\)-\(S\) space correspond to a heat engine or a heat pump?

      A clockwise path in \(T\)-\(S\) space corresponds to a heat engine. In each full cycle, there is more heat going into the working substance than heat leaving the working substance.

   3. Create a table, like the one below, and fill in all the values in terms of \(T_l\), \(T_h\), \(S_l\) and \(S_h\):

      Process	\(\Delta U\)	\(Q\)	\(W\)
      A
      B
      C
      D

      I first filled in the zeros. Then I filled in the non-zero \(\Delta U\) and \(Q\). Lastly, I used conservation of energy to determine \(W\).

      Process	\(\Delta U\)	\(Q\)	\(W\)
      A	0	\(+T_h\Delta S\)	\(-T_h\Delta S\)
      B	\(-\frac{3}{2}Nk\Delta T\)	0	\(-\frac{3}{2}Nk\Delta T\)
      C	0	\(-T_l\Delta S\)	\(+T_l\Delta S\)
      D	\(+\frac{3}{2}Nk\Delta T\)	0	\(+\frac{3}{2}Nk\Delta T\)

      where \(\Delta T = T_h - T_l\) and \(\Delta S = S_h - S_l\).

   4. If this cycle corresponds to a heat engine, find the efficiency in terms of \(T_h\) and \(T_l\). Alternatively, if this cycle corresponds to a heat pump, find the coefficient of performance in terms of \(T_h\) and \(T_l\).

      The efficiency of this cycle is give by \begin{equation} \eta = \frac{|W_{\text{net}}|}{Q_h}\\ \end{equation} where \(Q_h\) is the heat entering the substance during one cycle. \begin{align} \eta &= \frac{(T_h - T_l)\Delta S}{T_h\Delta S} \\ &= 1-\frac{T_l}{T_h} \end{align} This cyclic process is special/unique. It has the highest possible efficiency for a heat engine using thermal resevoirs at temperatures \(T_h\) and \(T_l\). The efficiency expression above is equivalent to the Carnot efficiency. It doesn't usually work out this way. Any other cyclic path through TS space would give a lower efficiency.

2. Helmholtz Free Energy of a Van Der Waals Gas S1 5076S The Helmholtz free energy of a van der Waals (vdW) gas can be written as: \begin{equation*} F=-N k T\left\{1+\ln \left[\frac{(V-N b) T^{\frac{3}{2}}}{N}\right]\right\}-\frac{a N^{2}}{V} \end{equation*} Where \(a\) and \(b\) are constants.
   1. Derive the equation of state (relationship between \(p\), \(T\), and \(V\)) for this Helmholtz free energy.
      Hint: The starting equations for this problem include the thermodynamic identity, the definition of Helmholtz free energy, \(F=U-TS\), and math identities such as the overlord equation.
      Bonus point: Rearrange the vdW equation of state to highlight any similiarites with the ideal gas equation of state (\(pV=NkT\)). To highlight similarities, group together terms that have dimensions of pressure, group together terms that have dimension of volume, etc.
   2. Using your expression from part (a), sketch or plot \(p(V)\) at various fixed temperatures. The volume axis should include \(Nb\) up to \(6Nb\). Your plot can be dimensionless (i.e. \(V/Nb\) on the x axis). Select values of \(NkT\) and \(aN^2\) that give curves with different shapes. Can you create a minima in pressure near \(V = 2Nb\)?

   As we did in the last homework we remember that \(dF=-SdT-pdV\), so that we can write: \begin{equation*} p=-\left(\frac{\partial F}{\partial V}\right)_{T} \end{equation*} We perform he derivative to obtain: \begin{equation*} p=-\left(\frac{\partial F}{\partial V}\right)_{T}=N k T\left(\frac{N}{(V-N b) T^{\frac{3}{2}}} \frac{T^{\frac{3}{2}}}{N}\right)-\frac{a N^{2}}{V^{2}}= \end{equation*} \begin{equation*} =N k T \frac{1}{V-N b}-\frac{a N^{2}}{V^{2}} \end{equation*} This can be re-organized as: \begin{equation*} \left(p+\frac{a N^{2}}{V^{2}}\right)(V-N b)=N k T \end{equation*} Which can be confirmed to be the van der Waals equation from, e.g., Wikipedia.

   Plotting the curve shapes on Desmos gives:

   

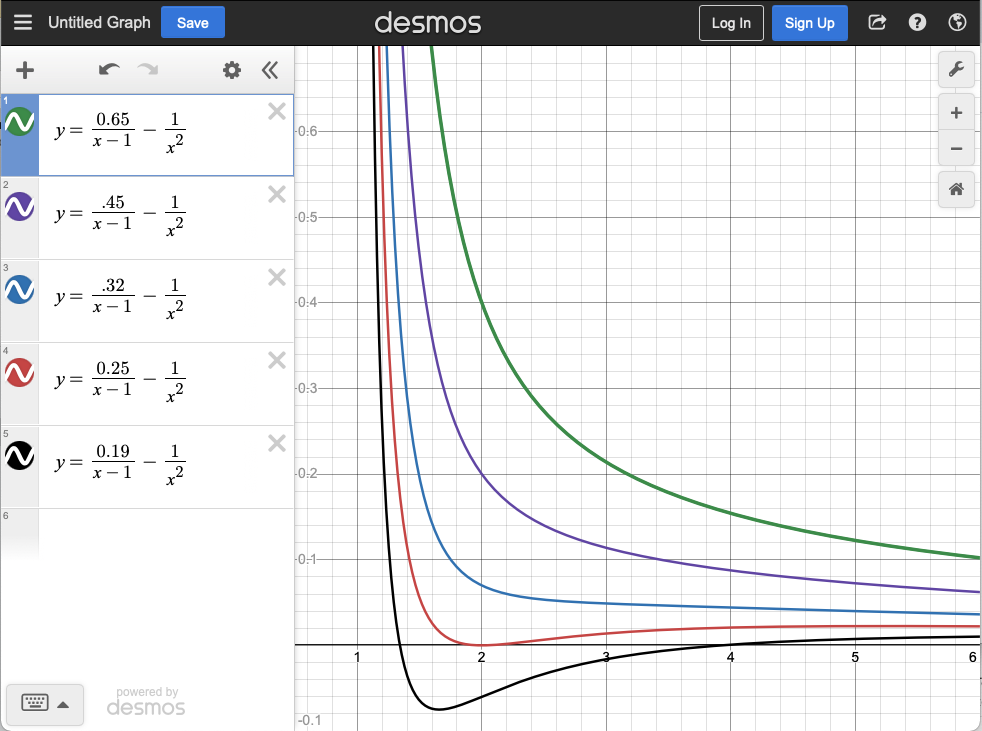
   Some of these curves go to negative pressure, which is interesting to think about. A system with negative pressure must be unstable. Systems will maximize their entropy, subject to any external constraints such as a container with fixed volume. A fluid or gas with negative pressure can increase its entropy by decreasing its volume. Such a system will spontaneously collapse until the pressure again becomes positive.