Static Fields: Winter-2025
HW 10 : Due 2/7 Fri

1. Confidence Rating S0 5186S After solving each problem on the assignment, indicate your answers to the following questions for each problem. Answer for the problem as a whole, even if the problem has multiple parts.
   1. Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?
      
      For the rest of the questions, assume you have interpreted the problem correctly
   2. Problem Confidence How confident are you that you could independently come up with a correct solution process to a similar problem on a future problem set?
      
   3. Answer Confidence How confident are you that your final answer to this question is correct (not solution process)?
      
   4. Makes Sense To what degree do you understand how your answer fits (or does not fit) the physical or mathematical situation of the problem?
      
2. Force and Torque on a Current Loop S0 5186S

   Consider a circular loop of wire carrying current \(I\) in a homogeneous (constant) magnetic field.

   The loop is in the \(xy\)-plane and the current goes in the counter-clockwise direction (if you're looking down onto the \(xy\)-plane). The magnetic field is \(\vec{B}=B_0 \left(\sin\alpha\, \hat{x}+\cos\alpha\, \hat{z}\right)\).

   1. (2pts) The Lorentz Force Law \[\vec{F}=q_{\hbox{test}} \left(\vec{E}+\vec{v}\times\vec{B}\right)\] says that the moving charges in the loop will experience a force due to the magnetic field.

      Rewrite the Lorentz Force Law as an integral over the current in the loop. Describe in words how you did the conversion, don't just look up a formula in a book.

   2. (4pts) Find the net force on the current loop.
   3. (4pts) Use the definition of torque \[\vec\tau =\vec{r}\times \vec{F}\] to find the net torque on the current loop (Hint: The torque is NOT zero. Think about which quantities in the definition of torque vary from point to point on the ring.)

3. Ampere's Law for a Cylinder S0 5186S In this problem, you will be investigating a cylindrical wire of finite radius \(R\), carrying a non-uniform current density \(J=\kappa s \;\hat{z}\), where \(\kappa\) is a constant and \(s\) is the distance from the axis of the cylinder.
   
   1. (2pts) Find the total current flowing through the wire.
      
   2. (2pts) Find the current flowing through Disk 2, a central (circular cross-section) portion of the wire out to a radius \(s_2<R\).
      

      

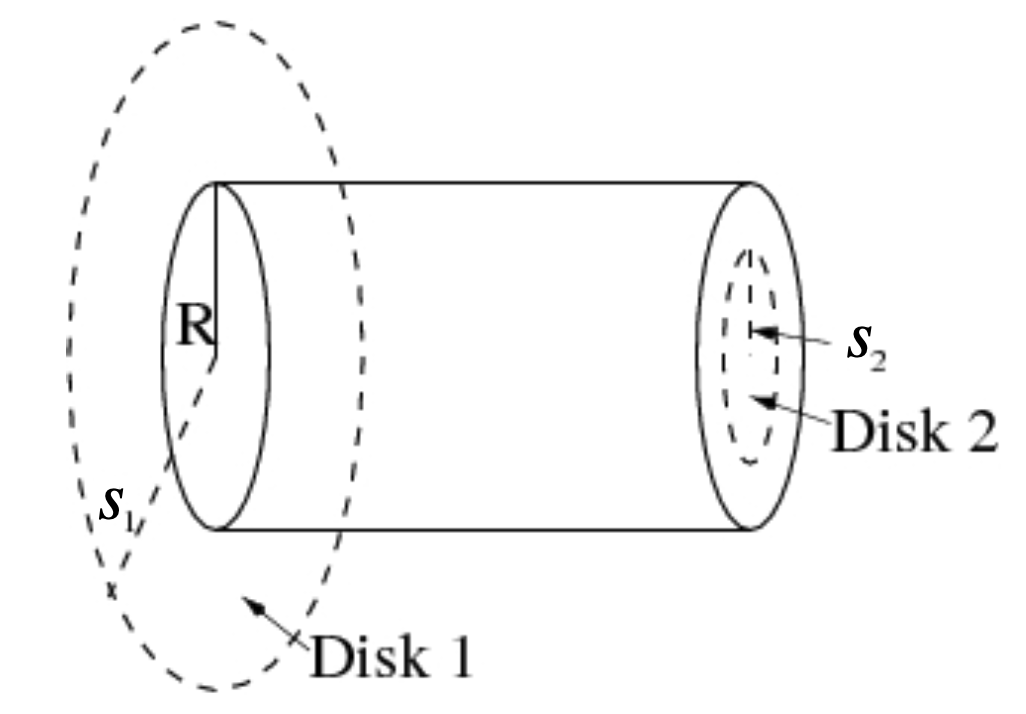
   3. (4pts) Use Ampere's law to find the magnetic field at a distance \(s_1\) outside the wire.
      
   4. (4pts) Use Ampere's law to find the magnetic field at a distance \(s_2\) inside the wire.
      
4. Magnetic Field and Current S0 5186S Consider the magnetic field \[ \vec{B}(s,\phi,z)= \begin{cases} 0&0\le s<a\\ \alpha \frac{1}{s}(s^4-a^4)\, \hat{\phi}&a<s<b\\ 0&s>b \end{cases} \]
   1. (2pts) Use step and/or delta functions to write this magnetic field as a single expression valid everywhere in space.
   2. (4pts) Find a formula for the current density that creates this magnetic field.
   3. (2pts) Interpret your formula for the current density, i.e. explain briefly in words where the current is.