Static Fields: Winter-2025
HW 04 : Due 1/17 Fri
- Distance Formula in Curvilinear Coordinates
S0 5164S
The distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\) and the point \(\vec r'\) is a coordinate-independent, physical and geometric quantity. But, in practice, you will need to know how to express this quantity in different coordinate systems.
Hint: Be sure to use the textbook: https://books.physics.oregonstate.edu/GSF/coords2.html
Find the distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\) and the point \(\vec r'\) in rectangular coordinates.
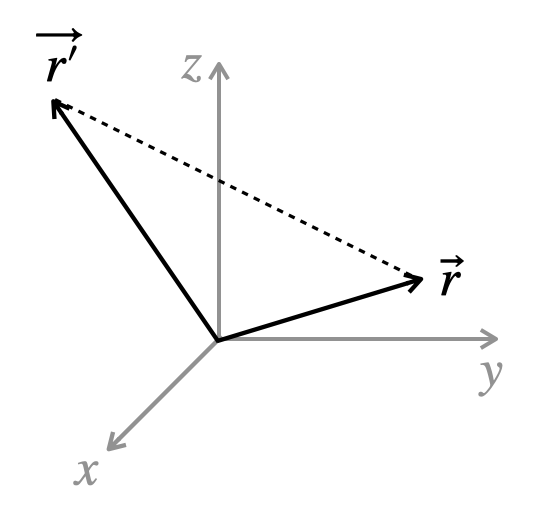
- The distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\,{}'=(x\,{}',y\,{}',z\,{}')\) and the point \(\vec r=(x,y,z)\) is a coordinate-independent, physical and geometric quantity. But, in practice, you will need to know how to express this quantity in different coordinate systems. Show that this same distance written in cylindrical coordinates is: \begin{equation*} \left|\vec r -\vec r\,{}'\right| =\sqrt{s^2+s\,{}'^2-2ss\,{}'\cos(\phi-\phi\,{}') +(z-z\,{}')^2} \end{equation*}
- Show that this same distance written in spherical coordinates is: \begin{equation*} \left\vert\vec r -\vec r\,{}'\right\vert =\sqrt{r'^2+r\,{}^2-2rr\,{}' \left[\sin\theta\sin\theta\,{}'\cos(\phi-\phi\,{}') +\cos\theta\cos\theta\,{}'\right]} \end{equation*}
- Now assume that \(\vec r\,{}'\) and \(\vec r\) are in the \(x\)-\(y\) plane. Simplify the previous two formulas.
- Triangle Parameters B
S0 5164S
(4 pts) Consider the function \(f(x)\) defined by: \begin{equation*} f(x) = 3x\,\theta(x)\,\theta(1-x)+(6-3x)\,\theta(x-1)\,\theta(2-x) \end{equation*} Make sketches of the following functions, by hand, on the axes with the same scale and domain. Briefly describe, using good scientific writing that includes both words and equations, the role that the number two plays in the shape of each graph:
\(y_1 = f(x)\)
\(y_2 = 2+f(x)\)
\(y_3 = f(2+x)\)
\(y_4 = 2f(x)\)
- \(y_5 = f(2x)\)
- Spherical Shell Step Functions
S0 5164S
One way to write volume charge densities without using piecewise functions is to use step \((\Theta)\) or \(\delta\) functions. Consider a spherical shell with charge density \[\rho (\vec{r})=\alpha3e^{(k r)^3} \]
between the inner radius \(a\) and the outer radius \(b\). The charge density is zero everywhere else.
- (2 pts) What are the dimensions of the constants \(\alpha\) and \(k\)?
- (2 pts) By hand, sketch a graph the charge density as a function of \(r\) for \(\alpha > 0\) and \(k>0\) .
- (2 pts) Use step functions to write this charge density as a single function valid everywhere in space.
- Volume Charge Density
S0 5164S
Consider the volume charge density: \begin{equation*} \rho (x,y,z)=c\,\delta (x-3) \end{equation*}
- (2 pts) Describe in words how this charge is distributed in space.
- (2 pts) What are the dimensions of the constant \(c\)?
- Confidence Rating
S0 5164S
After solving each problem on the assignment, indicate your answers to the following questions for each problem. Answer for the problem as a whole, even if the problem has multiple parts.
- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?

For the rest of the questions, assume you have interpreted the problem correctly - Problem Confidence How confident are you that you could independently come up with a correct solution process to a similar problem on a future problem set?

- Answer Confidence How confident are you that your final answer to this question is correct (not solution process)?

- Makes Sense To what degree do you understand how your answer fits (or does not fit) the physical or mathematical situation of the problem?

- Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?