Theoretical Mechanics: Fall-2021
Practice Acceleration in Polar Coordinates (SOLUTION): Due Day 16
- Acceleration in Polar Coordinates
S1 4099S
The acceleration vector written in polar coordinates is:
\[\vec{a} = \big[\ddot{s}-s\dot{\phi}^2\big]\hat{s}+\big[2\dot{s}\dot{\phi}+s\ddot{\phi}\big]\hat{\phi}\]
Below are motion diagrams, where each dot represents the location of a particle at equal time intervals.
For each motion diagram, indicate the direction of the acceleration vector at the middle dot (point 3) by sketching velocity vectors for points 2&4 and subtracting them.
Break the acceleration vector into polar components and match the components to terms in the acceleration equation above.
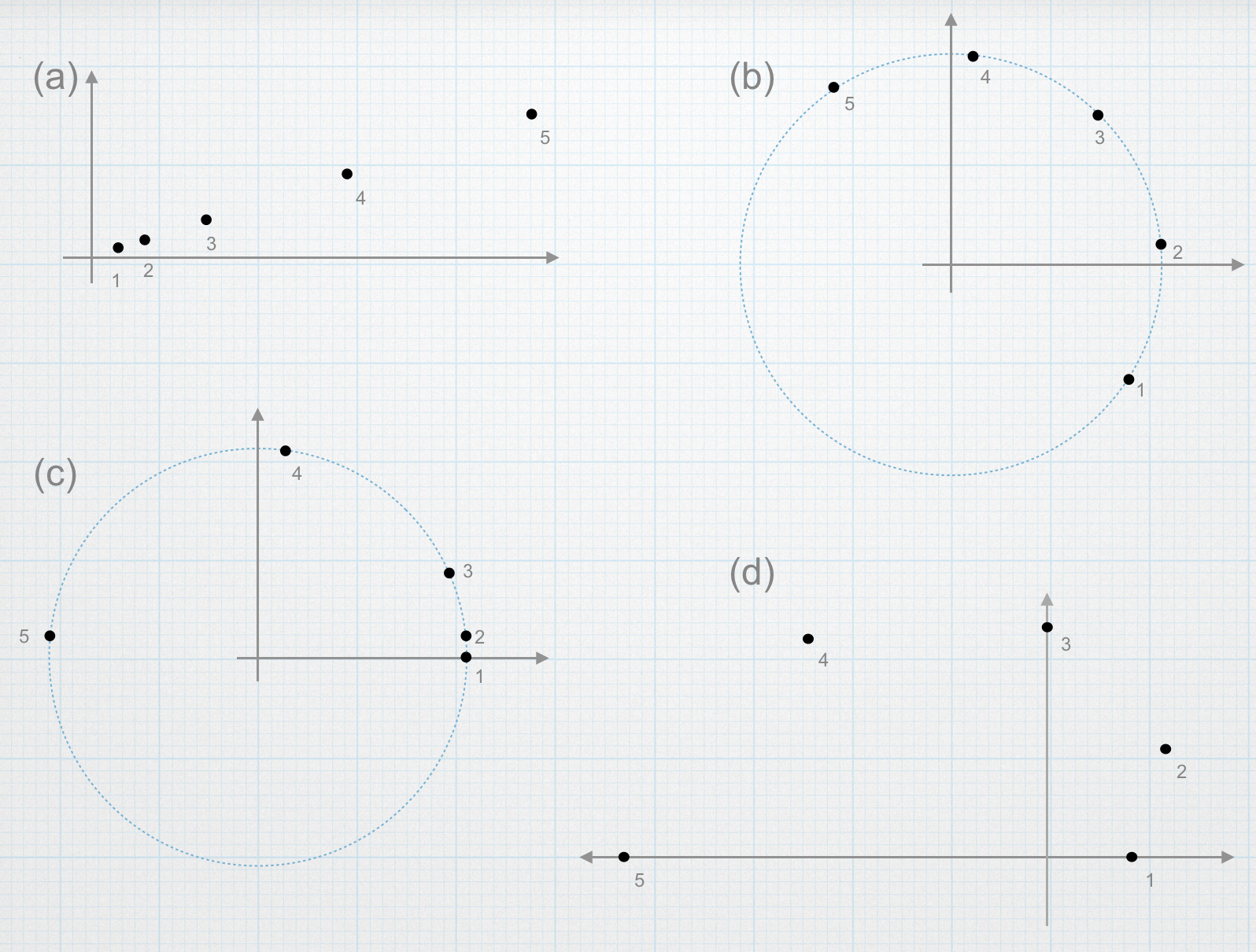
- The picture looks like:
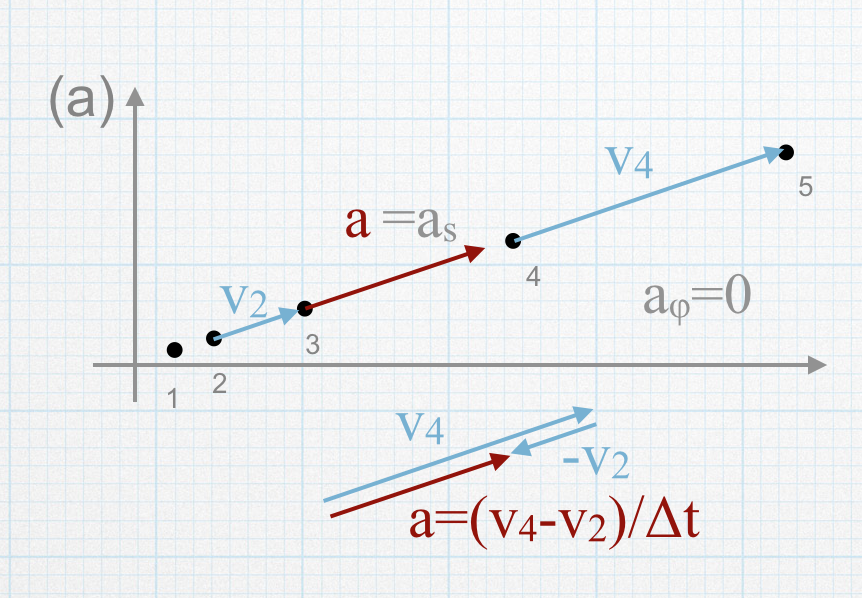
The particle is moving directly away from the origin, so \(\dot{\phi}=0\) and \(\ddot{\phi}=0\). The equation for the acceleration is: \[\vec{a} = \ddot{s}\hat{s}\] The acceleration only has a radial component. - The picture looks like:
 The particle is moving in a circle with constant angular speed, so \(\dot{s}=0\), \(\ddot{s}=0\), \(\dot{\phi}=\)constant, and \(\ddot{\phi}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}\]
The acceleration only has a radial (centripetal) component.
The particle is moving in a circle with constant angular speed, so \(\dot{s}=0\), \(\ddot{s}=0\), \(\dot{\phi}=\)constant, and \(\ddot{\phi}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}\]
The acceleration only has a radial (centripetal) component.
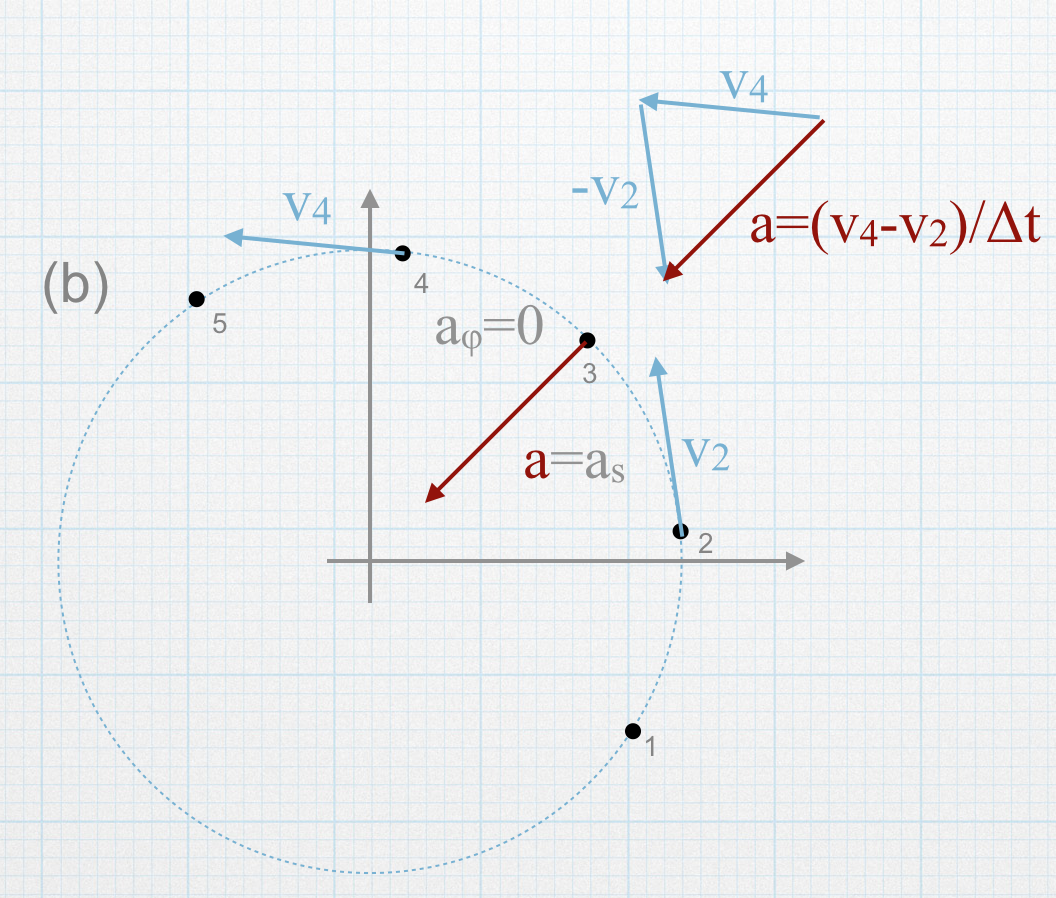
- The picture looks like:
 The particle is moving in a circle with an increasing angular speed, so \(\dot{s}=0\), and \(\ddot{s}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}+s\ddot{\phi}\hat{\phi}\]
The acceleration only both a radial (centripetal) component and a tangential component corresponding to the increasing speed of the particle.
The particle is moving in a circle with an increasing angular speed, so \(\dot{s}=0\), and \(\ddot{s}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}+s\ddot{\phi}\hat{\phi}\]
The acceleration only both a radial (centripetal) component and a tangential component corresponding to the increasing speed of the particle.
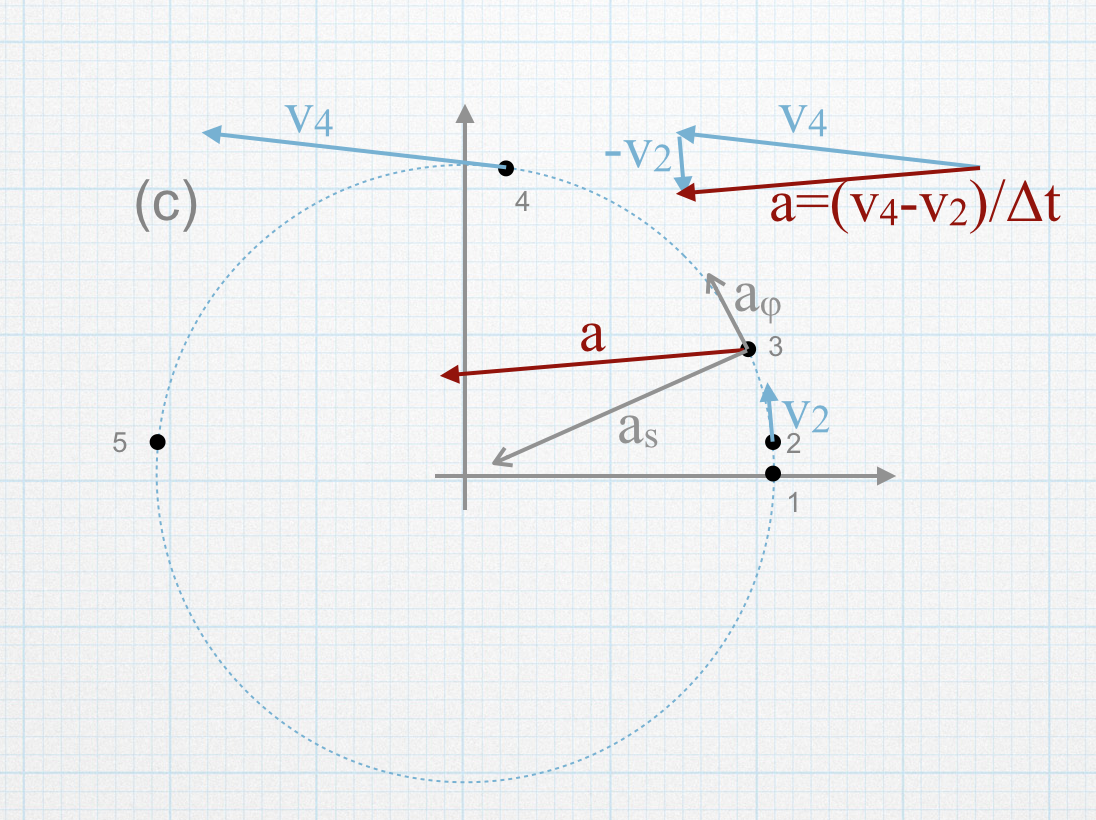
- The picture looks like:
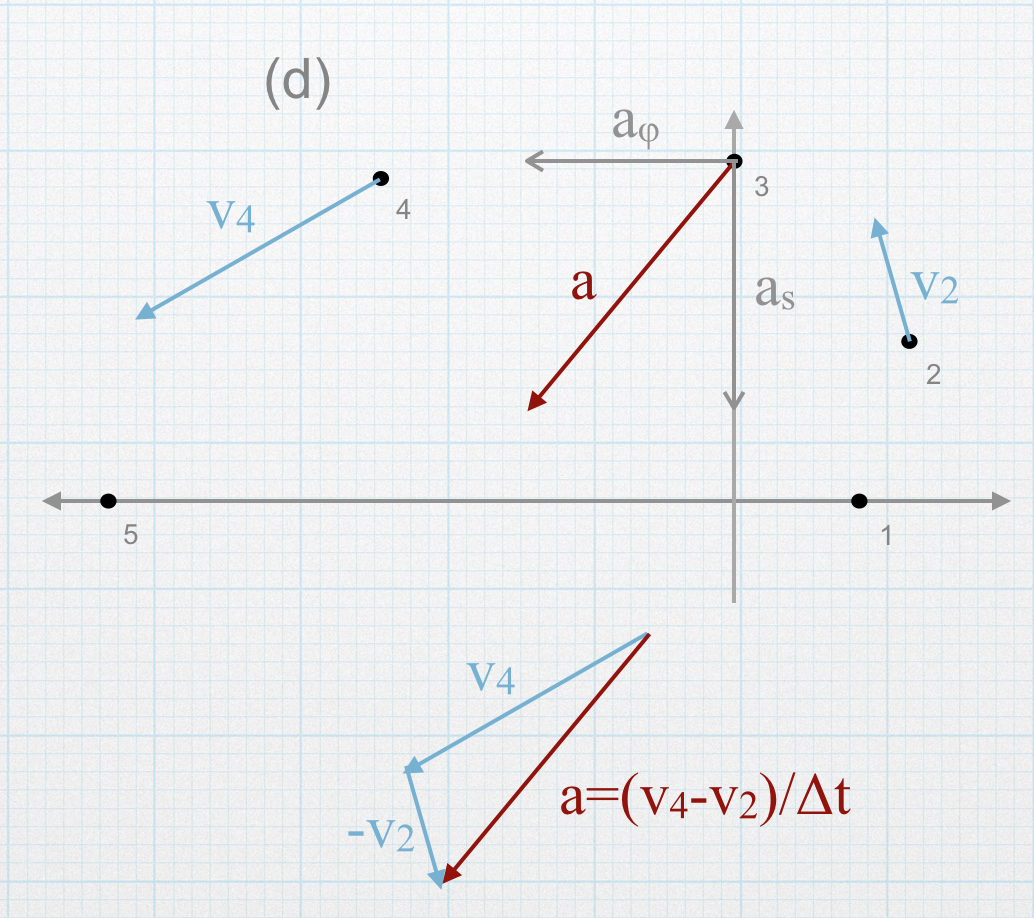 The particle is moving around but away from the origin so \(\dot{s}\neq0\). The radius of the motion increases the same amount in each time interval, so \(\ddot{s}=0\). The angular displacement is \(\pi/4\) for each time interval so the angular velocity is constant, so \(\ddot{\phi}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}+2\dot{s}\dot{\phi}\hat{\phi}\]
The acceleration only both a radial (centripetal) component and a tangential Coriolis component corresponding to the changing direction of radial component of the velocity vector as the particle moves around the origin.
The particle is moving around but away from the origin so \(\dot{s}\neq0\). The radius of the motion increases the same amount in each time interval, so \(\ddot{s}=0\). The angular displacement is \(\pi/4\) for each time interval so the angular velocity is constant, so \(\ddot{\phi}=0\). The equation for the acceleration is:
\[\vec{a} = s\dot{\phi}^2\hat{s}+2\dot{s}\dot{\phi}\hat{\phi}\]
The acceleration only both a radial (centripetal) component and a tangential Coriolis component corresponding to the changing direction of radial component of the velocity vector as the particle moves around the origin.
- The picture looks like: