Theoretical Mechanics: Fall-2021
Curvilinear Coordinates Practice (SOLUTION): Due Day 16
- Speed Squared in Curvilinear Coordinates
S1 4098S
Show that the speed squared written in different standard coordinates systems is:
in rectangular coordinates: \(v^2 = \dot{x}^2 + \dot{y}^2+\dot{z}^2\)
\begin{align*} v^2 &= \vec{v} \cdot \vec{v}\\ &= (\dot{x}\hat{x}+\dot{y}\hat{y}+\dot{z}\hat{z}) \cdot (\dot{x}\hat{x}+\dot{y}\hat{y}+\dot{z}\hat{z})\\ &= \dot{x}^2 + \dot{y}^2+\dot{z}^2 \checkmark \end{align*}
in cylindrical coordinates: \(v^2 = \dot{s}^2 + s^2\dot{\phi}^2+\dot{z}^2\)
First approach:
\begin{align*} x &= s \cos \phi\\ \dot{x} & = \dot{s}\cos\phi - s\sin\phi\dot\phi \\[6pt] y &= s \sin \phi \\ \dot{y} &= \dot{s}\sin\phi + s\cos\phi\dot\phi \\[6pt] z &= z\\ \dot{z} &= \dot{z} \\[6pt] v^2 &= \dot{x}^2 + \dot{y}^2+\dot{z}^2 \\ &= (\dot{s}\cos\phi - s\sin\phi\dot{\phi})^2\\ &+ (\dot{s}\sin\phi + s\cos\phi\dot{\phi})^2\\ &+\dot{z}^2 \\[6pt] v^2 &= \dot{s}^2\color{red}{\cos^2\phi} + s^2\color{blue}{\sin^2\phi}\dot{\phi}^2 \cancel{- 2 s\dot{s}\dot{\phi}\sin\phi\cos\phi} \\ & + \dot{s}^2\color{red}{\sin^2\phi} + s^2\color{blue}{\cos^2\phi}\dot{\phi} + \cancel{2 s\dot{s}\dot{\phi}\sin\phi\cos\phi}\\ & + \dot{z}^2 \\[6pt] &= \dot{s}^2 \cancelto{1}{\color{red}{(\cos^2\phi + \sin^2\phi)}} + s^2 \dot{\phi}^2 \cancelto{1}{\color{blue}{(\sin^2\phi + \cos^2\phi)}} + \dot{z}^2 \\[6pt] &= \dot{s}^2 + s^2 \dot{\phi}^2 + \dot{z}^2 \checkmark \end{align*}
in spherical coordinates: \(v^2 = \dot{r}^2 + r^2\dot{\theta}^2+r^2\sin^2\theta\dot{\phi}^2\)
First approach:
\begin{align*} x &= r \cos\phi \sin\theta\\ \dot{x} & = \dot{r} \cos\phi \sin\theta - r \sin\phi \dot\phi \sin\theta + r \cos\phi \cos\theta \dot{\theta} \\[6pt] y &= s \sin \phi \sin\theta \\ \dot{y} &= \dot{r} \sin\phi \sin\theta + r \cos\phi \dot\phi \sin\theta + r \sin\phi \cos\theta \dot{\theta} \\[6pt] z &= r \cos\theta \\ \dot{z} &= \dot{r} \cos\theta - r \sin\theta \dot{\theta} \\[6pt] v^2 &= \dot{x}^2 + \dot{y}^2+\dot{z}^2 \\ &= (\dot{r} \cos\phi \sin\theta - r \sin\phi \dot{\phi} \sin\theta + r \cos\phi \cos\theta \dot{\theta})^2\\ &+ (\dot{r} \sin\phi \sin\theta + r \cos\phi \dot{\phi} \sin\theta + r \sin\phi \cos\theta \dot{\theta})^2\\ &+ (\dot{r} \cos\theta - r \sin\theta \dot{\theta})^2 \\[6pt] v^2 &= \dot{r}^2 \color{red}{\cos^2\phi} \sin^2\theta + r^2 \color{blue}{\sin^2\phi} \dot{\phi}^2 \sin^2\theta + r^2 \color{green}{\cos^2\phi} \cos^2\theta \dot{\theta}^2 \\ & \cancel{- 2r\dot{r} \sin\phi \cos\phi \sin^2\theta} - \bcancel{2r \dot{r}\sin\phi \cos\phi \dot{\phi} \dot{\theta} \sin\theta \cos\theta} + 2r \dot{r} \color{purple}{\cos^2\phi} \dot{\theta} \sin\theta \cos\theta \\ & + \dot{r}^2 \color{red}{\sin^2\phi} \sin^2\theta + r^2 \color{blue}{\cos^2\phi} \dot{\phi}^2 \sin^2\theta + r^2 \color{green}{\sin^2\phi} \cos^2\theta \dot{\theta}^2 \\ & \cancel{+ 2r\dot{r} \sin\phi \cos\phi \sin^2\theta} + \bcancel{2r^2 \sin\phi \cos\phi \dot{\phi} \dot{\theta} \sin\theta \cos\theta} + 2r \dot{r} \color{purple}{\sin^2\phi} \dot{\theta} \sin\theta \cos\theta \\ & + \dot{r}^2 \cos^2\theta +r^2 \sin^2\theta \dot{\theta}^2 -2r \dot{r} \sin\theta \cos\theta \dot{\theta} \\[6pt] &= \dot{r}^2 \color{magenta}{\sin^2\theta} \cancelto{1}{\color{red}{(\cos^2\phi + \sin^2\phi)}} + r^2 \dot{\phi}^2 \sin^2\theta \cancelto{1}{\color{blue}{(\sin^2\phi + \cos^2\phi)}} + r^2 \color{orange}{\cos^2\theta} \dot{\theta}^2 \cancelto{1}{\color{green}{(\sin^2\phi + \cos^2\phi)}} \\ & \bcancel{2r\dot{r}\dot{\theta}\sin\theta\cos\theta} \cancelto{1}{\color{purple}{(\cos^2\phi + \sin^2\phi)}} \\ & + \dot{r}^2 \color{magenta}{\cos^2\theta} +r^2 \color{orange}{\sin^2\theta} \dot{\theta}^2 \bcancel{-2r \dot{r} \sin\theta \cos\theta \dot{\theta}} \\[6pt] &= \dot{r}^2 \cancelto{1}{\color{magenta}{(\sin^2\theta + \cos^2\theta)}} + r^2 \dot{\phi}^2 \sin^2\theta + r^2 \cancelto{1}{\color{orange}{(\cos^2\theta + \sin^2\theta)}}\dot{\theta}^2\\ &= \dot{r}^2 + r^2 \dot{\theta}^2 + r^2 \sin^2\theta \dot{\phi}^2 \checkmark \end{align*}
where:
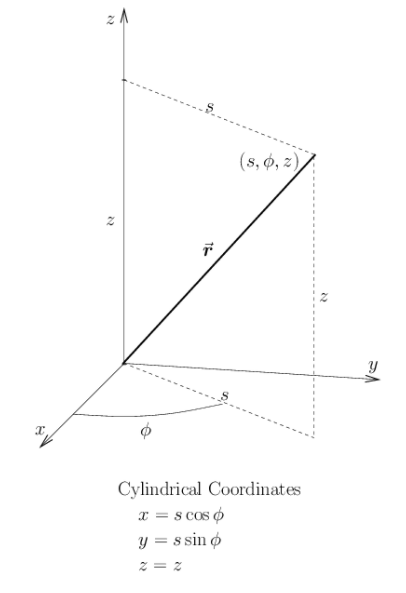
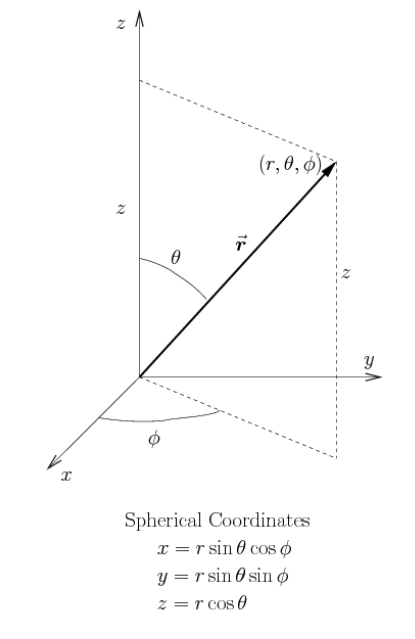
The algebra for these calculations is a little tedius, but it's good to do them once in your career to convince yourself that these expressions are true!
See: GMM: Curvilinear Coordinates for more discussion of curvilinear coordinates. Note that the labels for the aximuthal and polar coordinates in different for math and physics (\(\phi\) and \(\theta\) are swapped.)