Theoretical Mechanics: Fall-2021
Practice Power Series (SOLUTION): Due Day 14

1. Power Series Practice S1 4094S
   1. Calculate the \(n=0, 1, 2, 3, 4\) coefficients of the power series for \(\cos{z}\) expanded around \(z=\pi\). Using these coefficients, find a power series approximation for this function.
      

      First, the form of the answer will be: \[ \cos z \approx c_0 + c_1 (z-\pi) + c_2 (z-\pi)^2 + c_3(z-\pi)^3 + c_4(z-\pi)^4\]

      Because I'm asked for the fourth order expansion, I'll keep only terms with power 4 or less.

      Now, to calculate the coefficients: \begin{eqnarray*} c_0 &=& \frac{1}{0!}f(z=z_0) = \cos\pi = -1 \\ c_1 &=& \frac{1}{1!}\left.\frac{df}{dz}\right|_{z=z_0} = -\sin \pi = 0 \\ c_2 &=& \frac{1}{2!}\left.\frac{d^2f}{dz^2}\right|_{z=z_0} = -\frac{1}{2}\cos \pi = \frac{1}{2} \\ c_3 &=& \frac{1}{3!}\left.\frac{d^3f}{dz^3}\right|_{z=z_0} = \frac{1}{6}\sin \pi = 0 \\ c_4 &=& \frac{1}{4!}\left.\frac{d^4f}{dz^4}\right|_{z=z_0} = \frac{1}{24}\cos \pi = -\frac{1}{24} \\ \end{eqnarray*}

      So, the approximation I end up with is:

      \[ \cos z \approx -1 + \frac{1}{2} (z-\pi)^2 +-\frac{1}{24}(z-\pi)^4\]

   2. Plot both the original function and your approximation.

      Here is the code in Mathematica and the graph it produces.

      

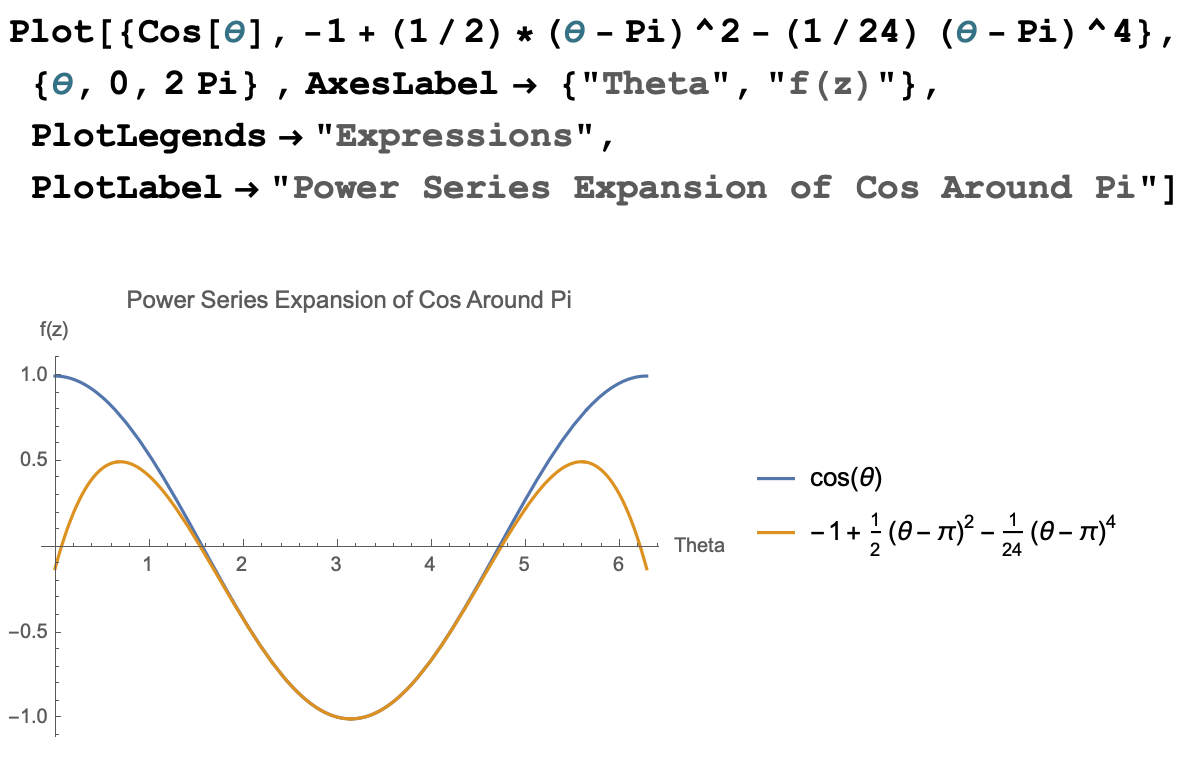
   3. For what values of \(z\) is your approximation “good”?

      When I plot this approximation against the cosine function, I see that the expansion approximates the cosine function reasonably well between about \(\pi/2\) and \(3\pi/2\).