Theoretical Mechanics: Fall-2021
Practice Zapping with d (SOLUTION): Due Day 12
- Shooting a Box
S1 4091S
Suppose the spaceship is approaching the Earth at \(3c/5\) and shoots a box at a speed of \(4c/5\) (from the spaceship's perspective).
At what velocity will an Earth-bound observer see the box if it is shot directly towards the Earth?
\(\frac{35c}{37}\)
- Sensemaking: Reasonable Value
Briefly discuss why (or why not) your answer seem reasonable.
- Zapping with d
S1 4091S
Zap the following equations with “d”:
\(f= 3x^3-e^{2x}\)
\(df=(9x^2-2e^{2x})\, dx\)
\(g = \sin(y^2)\)
\(dg = \cos{(y^2)}\, 2y\,dy\)
- \(5z^4 = \ln(p)\)
\(20\, z^3\, dz = \frac{1}{p} \, dp\)
- Relativistic Explosion
S1 4091S
A lump of clay with mass \(M\) explodes into two equal pieces \(m\) moving directly away from each other.
What is the speed of each of the pieces after the explosion?
Using momentum conservation:
\begin{align*} \vec{p}_i &= \vec{p_f} \\[6pt] \begin{bmatrix} 0\\ Mc \end{bmatrix} =& \begin{bmatrix} \gamma m v\\ \gamma m c \end{bmatrix} + \begin{bmatrix} -\gamma m v\\ \gamma m c \end{bmatrix}\\ \\ \end{align*}
Looking at the second entries only:
\begin{align*} Mc &= 2\gamma mc \\ \gamma &= \frac{M}{2m} \\ \frac{1}{\sqrt{1-(v/c)^2}} &= \frac{M}{2m} \\ 1-(v/c)^2 &= \frac{4m^2}{M^2} \\ v/c &= \sqrt{1-\frac{4m^2}{M^2}} \\ \end{align*}
- Sensemaking: Check a Special Case
Conceptually, what would you expect the speed of the lumps to to be if \(m=\frac{M}{2}\)? Show that your answer to part (a) works for this special case. - What is the relativisic kinetic energy of each of the pieces?
The total relativistic kinetic energy of the two pieces is the rest energy of the initial clump minus the rest energy of the two pieces. \begin{align*} 2T = (M-2m)c^2 \\ T= \frac{(M-2m)c^2}{2} \end{align*}
- Moving Clocks Run Slow
S1 4091S
Imagine that you have a light clock with a period T (1 “tick” takes time \(T\)).
Another observer moves relative to you with velocity \(+V\)
- Draw a spacetime diagram of 1 tick of the your light clock.
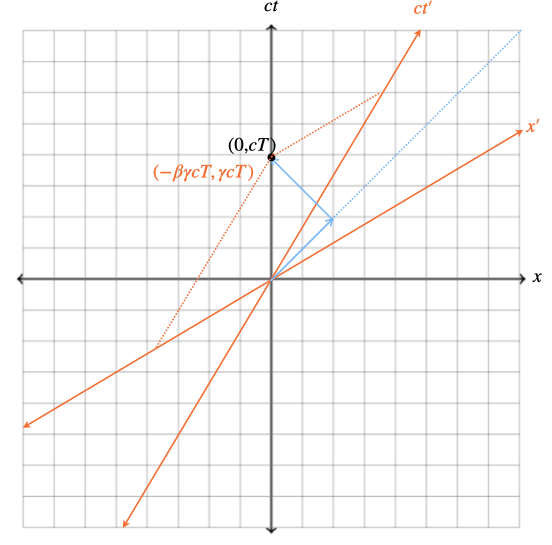
- What are the spacetime coordinates of the end of the “tick” of your light clock in:
Your reference frame?
\begin{align*} \begin{bmatrix} x_{mine}\\ ct_{mine} \end{bmatrix} = \begin{bmatrix} 0\\ cT \end{bmatrix} \end{align*}
The other observer's frame?
\begin{align*} \begin{bmatrix} x'_{mine}\\ ct'_{mine} \end{bmatrix} = \begin{bmatrix} \gamma & -\beta\gamma \\ -\beta\gamma & \gamma \end{bmatrix} \begin{bmatrix} 0\\ cT \end{bmatrix} = \begin{bmatrix} \gamma cT\\ -\beta \gamma cT \end{bmatrix} \end{align*}
Now image that the other observer has an identical light clock. Draw a new spacetime diagram of 1 “tick” of the other observer's light clock.
The diagram could looks like one of the following:
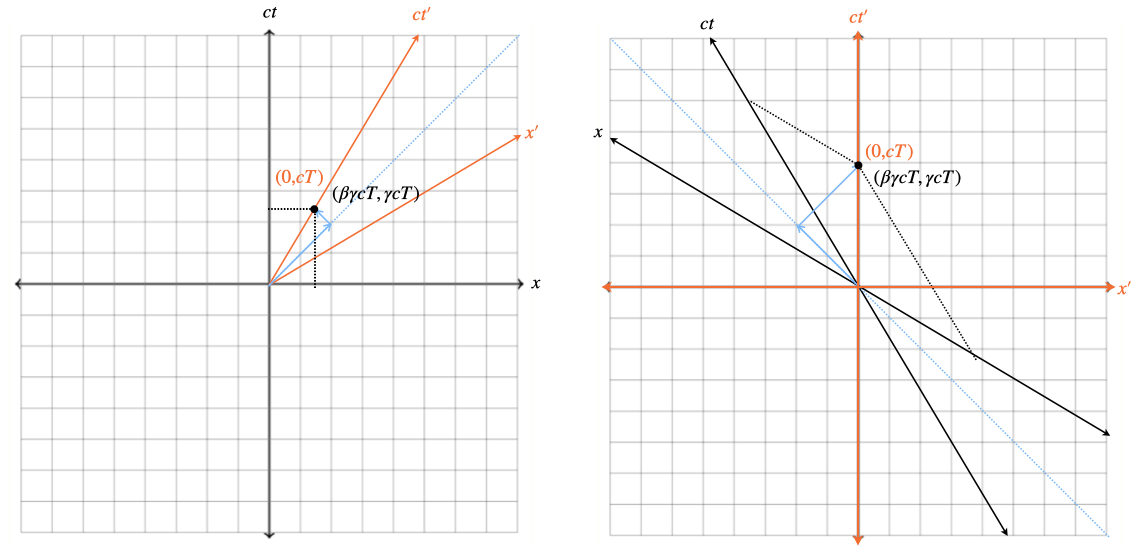
- What are the spacetime coordinates of the end of the “tick” of the other observer's light clock in:
The other observer's frame?
\begin{align*} \begin{bmatrix} x'_{theirs}\\ ct'_{theirs} \end{bmatrix} = \begin{bmatrix} 0\\ cT \end{bmatrix} \end{align*}
Your reference frame?
\begin{align*} \begin{bmatrix} x_{theirs}\\ t_{theirs} \end{bmatrix} = \begin{bmatrix} \gamma & +\beta\gamma \\ +\beta\gamma & \gamma \end{bmatrix} \begin{bmatrix} 0\\ cT \end{bmatrix} = \begin{bmatrix} \gamma cT\\ \beta \gamma cT \end{bmatrix} \end{align*}
- Sensemaking: Tell a Conceptual Story
Imagine that one of your classmates says, “Moving clocks run slow.” Do you agree? Explain your reasoning.If I compare the time coordinates of the tick of my friend's clock, I see the tick take \(\gamma cT\) while the other observer sees a shorter time \(cT\). Since I observe the tick taking a longer time that the other observer does, I say that their clock is running slow.
Similarly, if if I compare the time coordinates of the tick of my clock, I see the tick take \(cT\) while the other observer sees a longer time \(\gamma cT\). Since my clock is moving relative to the other observer, and they observe a longer time interval for the tick than I do, the other observer observes my clock running slow.

- Draw a spacetime diagram of 1 tick of the your light clock.