Theoretical Mechanics: Fall-2021
HW 9 : Due
- Atwood Machine
S0 4100S
Consider an Atwood machine, in which two blocks \(m_1\) and \(m_2\) are suspended by an inextensible string (length \(l\)) which passes over a pulley with moment of inertia \(I\) and radius R. The pulley has frictionless bearings.
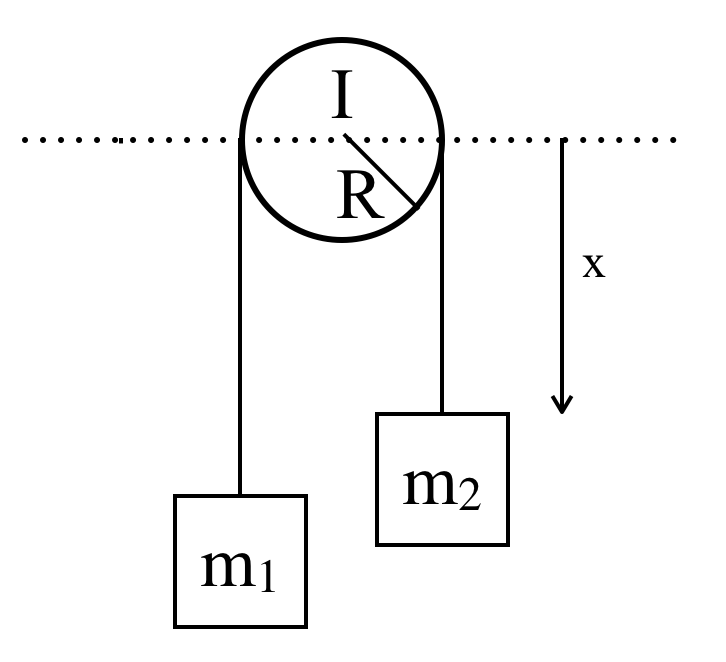
Starting from Newton's 2nd Law, find the acceleration of the system.
- Write down the Lagrangian of the system and use it to find the acceleration of the system. (Do you get the same answer?)
- Use 3 sensemaking strategies to evaluate your answer.
- Bead on a Rotating Rod
S0 4100S
(modified from Taylor 7.21)
The center of a long frictionless rod is pivoted at the origin, and the rod is forced to rotate in a horizontal plane with constant angular velocity \(\omega\). Consider a bead with mass \(m\) that is free to move frictionlessly along the rod. Find the position of the bead as a function of time using the polar coordinate \(s\) as your generalized coordinate.
- Using a Lagrangian approach, find the position of the bead as a function of time using the polar coordinate \(s\) as your generalized coordinate.
- Use 3 sensemaking strategies to evaluate your answer. (Be sure to articulate your expected results during each strategy.)
- Bead on a Helix 1
S0 4100S
(adapted from Taylor 7.20)
A smooth wire is bent into the shape of a helix, with cylindrical polar coordinates \(s=R\) and \(z=\lambda\phi\), where \(R\) and \(\lambda\) are constants and \(z\) is vertically up (and gravity vertically down). Using \(z\) as your generalized coordinate, write down the Lagrangian for a bead of mass \(m\) threaded on the wire.
Find the bead's vertical acceleration \(\ddot{z}\).
Use three sensemaking strategies to evaluate your answer to part (a). (Don't forget to articulate your expected result for each strategy.)
In the limit that \(\lambda\rightarrow 0\), what is \(\ddot{z}\)? Explain conceptually how this makes sense.
- How does the acceleration depends on the parameters of the problem (\(R\) and \(\lambda\))? Plot the \(\ddot{z}\) vs. \(R\) and \(\ddot{z}\) vs. \(\lambda\). Explain what these plots tell you about how the geometry of the helix affects the acceleration.
- Generalized Force and Generalized Momentum S0 4100S Demonstrate that when your generalized coordinate is an angle, the generalized force associated with that coordinate is a torque and that the generalized momentum associated with that coordinate is an angular momentum.