Theoretical Mechanics: Fall-2021
HW 6 : Due
- The Twin Paradox
S0 4093S
(modified from Griffiths 12.16)
On their 21st birthday, one twin, Alex, gets on a moving sidewalk, which carries her out to star X at speed \(4/5c\). Her twin brother, Blake, stays home. When Alex gets to star X, she immediately jumps onto the returning (inbound) moving sidewalk and comes back to earth, again at speed \(4/5c\). She arrives on her 39th birthday (as determined by her watch).
What is potentially paradoxical about this situation?
You're going to resolve this paradox using a Spacetime diagram and Lorentz transformations. Draw a single spacetime diagram showing the entire trip in the reference frame of Blake. Your diagram should show the world lines of both twins. Label all events and show the space and time axes of the different frames. Update your spacetime diagram as you answer the following questions.
How old is Blake (who stayed at home)?
From Blake's perspective, how far away is star X? (Give your answer in light years.)
Now, we're going to use a trick: we're going to recognize that Alex actually switches reference frames at Star X, and we're going to calibrate this “inbound” reference frame the same as the other two frames. We'll call the outbound sidewalk system \(S'\) and the inbound one \(S''\) (the earth system is \(S\)). All three frames synchronize their their master clocks and choose their origins at the location of Earth so that all the origins are colocated at \(t=t'=t''=0\)
What are the coordinates \((x, ct)\) of the jump (from the outbound to inbound sidewalk) in \(S\) (Blake's frame)?
What are the coordinates \((x', ct')\) of Alex's jump in \(S'\) (Alex's outbound frame)?
What are the coordinates \)(x”, ct”)\( of the jump in \)S”\( (Alex's inbound frame)?
If Alex wanted her watch to agree with the clock in \)S”\(, how would she have to reset it immediately after the jump? (In other words, what is the time of the jump in the \)S”\( frame.) If she \textit{did} this, what would her watch read when she got home? (This wouldn't change her \textit{age}, of course---she's still 39---it would just make her watch agree with the standard synchronization in \)S”\(.
- If Alex is asked the question, “What is Blake's age on Earth right now?”, what is the correct reply:
just before she makes the jump?
just after she makes the jump?
(Hint: You need to consider an event at Blake's location that is simultaneous (from Alex's perspective) with the jump.)
How many earth years does the return trip take? Add this to (ii) from (I) to determine how old Alex expects Blake to be at their reunion.
- How is the paradox resolved?
- Projectile Over Incline
S0 4093S
(modified from Taylor 1.39)
The physics of this problem is at the introductory level, but the problem might be more advanced than what you did in that course. I want you to solve the problem in terms of the symbolic parameters I've given in the problem (and other constants). The incline of the ground is a parameter that we'll allow to vary.
The main purpose of this problem is to practice strategies for making sense of your answer: checking dimensions, thinking about the behavior of functions, evaluating special cases. For all of these strategies, you'll first anticipate what the dimensions/beasts, behaviors, special cases are based on your conceptual knowledge of the problem situation and similar problems you've solved in the past. Then you'll make the calculations. Last you'll "check" the results of your calculations against your anticipations. The anticipations are the hardest part. You won't be graded down for making incorrect anticipations, but if they're wrong, you need to say that when you compare them to your calculations. (and it will help your learning if you try to understand why your anticipations were wrong.)
Problem: A ball is thrown into the air, but the ground below is not flat - it makes an angle \(\phi\) above the horizontal. The ball initially moves uphill with speed \(v_0\) at an angle \(\theta\) above the unlevel ground. Choose perpedicular axes with \(x\) measured directly up the slope of the ground, \(y\) normal to the ground, and \(z\) horizontal.
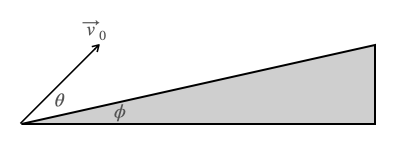
Anticipate Dimensions and Beasts of the Position: Before solving for the equations of motion, state what dimensions (not units) and “beast” (mathematical entity) you expect for the position. (In the future, you should check dimensions in every calculation and even in intermediate steps).
Calculate the Equations of Motion: Use Newton's second law to find the position of the projectile as a function of time.
Check Dimensions and Beasts: What “beast” (mathematical entity) is your answer? What dimensions (not units) does your answer have? Do these match your anticipations?
Anticipate the Functional Behavior: What variables do you expect the range of the projectile (your answer to part (f)) to depend on? As you vary one of those variables how do you expect the range to change and why? Repeat for each variable.
Calculate the Range: Calculate the range of the ball (i.e., the distance traveled along the unlevel ground). Use trig identities to simplify your results as much as possible.
Check Functional Behavior: Do the variables that appear in the range equation you found match those that you expected? Choose arbitrary (not special) and realistic values for \(v_0\) and \(\phi\) and plot (with a computer) the range as a function of initial angle over the ground. Does the behavior you plot match the behavior you expected?
Anticipate Special Cases: In the next part you will calculate the maximum range of the projectile for different values of \(\phi\). Are there special values of \(\phi\) where you might already know what the maximum range (distance traveled along the unlevel ground) might be? What are those values of \(phi\), what does the ground look like, and what would be the maximum range in that case?
Calculate the Maximum Range: Calculate the maximum range of the ball as a function of \(\phi\) (the max range is different for inclines with different slopes). Use trig identities to simplify your results as much as possible.
Check the Special Cases: Evaluate the values of the special cases you identified in part (h). What answers do you get? Are those answers consistent with familiar problems and why? Explain any discrepancies. Be sure to analyze when the ground is horizontal and vertical.