Contemporary Challenges: Spring-2025
HW Week 9 : Due 27 Friday
- Photons per second from laser S0 5267S (Q4B.4 from textbook) A typical laboratory helium-neon laser produces about 1 mW (0.001 J/s) of light at a wavelength of 633 nm. How many photons per second does this laser produce?
- Seeing stars
S0 5267S
Our sun radiates light energy at a rate of \(P_{\text{sun}} = 4\times 10^{26}\text{ J/s}\). Assume that most of this energy is yellow light. Estimate how far away a star like the sun could be from Earth and still be seen by an unaided human eye. Assume the diameter of the pupil is 8 mm when dilated (looking at the night sky).
Sense making: Most stars we see in the sky are hundreds of light years away. What does this say about the luminosity (total power of visible light) from most of the stars that we see?
Reminder: a photoreceptor in the eye requires about 500 photons within a 30 ms time period to observe something.
- Light from an electron in a box
S0 5267S
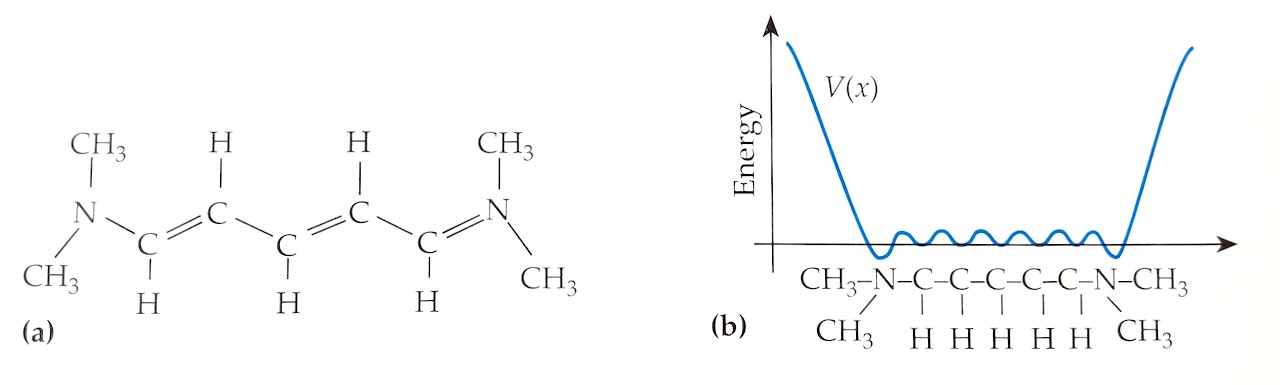
Suppose an electron is trapped in a box whose length is \(L= 1.2 \text{ nm}\). This is a coarse-grained model for an electron in a small molecule like cyanine (see Example Q11.1 in the textbook, and the figure above). If we solve the Schrodinger equation for this coarse-grained model, the possible energy levels for this electron are \begin{align} E = \frac{h^2 n^2}{8 m L^2} \end{align} where \(m\) is the mass of the electron and \(n= 1,\ 2,\ 3,\ ...\)
Draw a spectrum chart (like the righthand side of Figure Q11.2) to show what you would see if a number of identical excited systems of this type emitted light that was dispersed by a diffraction grating.
Note: Due to the shape/symmetries of electron wavefunctions in a box, optical transitions between energy levels only happen when \(\Delta n = n_\text{initial}-n_\text{final}\), is an odd integer.

- Efficiency of a solar cell
S0 5267S
Download the file extraterr_solar.csv, which is in comma-separated-variable (csv) format. Open the csv file in a spreadsheet program such as Excel. The data is the spectral intensity with respect to wavelength, \(S_\lambda\), for the sunlight that is hitting a satellite above the earth. The first column is wavelength in units of nanometers. The second column is spectral intensity in units of W/(m\(^2\cdot\)nm).
- Use a spreadsheet to perform a simple numerical integration (Riemann sum) to find the total energy flux hitting the satellite. Explain your method using summation notation. Additionally, write down the formula you enter in the spreadsheet (e.g. =SUM(B1:B745)). Give your final answer in units of W/m\(^2\) and check that it is reasonable.
Consider a narrow band of wavelengths, from 552.5 nm to 557.5 nm. (The bandwidth is 5 nm and the central wavelength is 555 nm). All the photons in this bandwidth have very similar energy, \(E_{\text{photon}} \approx\) (1240 nm\(\cdot\)eV)/(555 nm). How many photons per second per \(\text{m}^2\) are in this spectral band of sunlight? Explain your method using standard mathmeatical notation. Additionally, write down the formula that you entered into the spreadsheet.
The calculation that you did for part b can now be applied to every row in your spreadsheet. You will need these numbers for part c.
- Silicon solar cells absorb photons if \(E_{\text{photon}}> 1.1\text{ eV}\). That is to say, \(E_{\text{photon}}\) must be greater than gap between occupied and unoccupied quantum energy levels in silicon. Use your spreadsheet to calculate how many photons per second per \(\text{m}^2\) have sufficient energy to be absorbed by a solar cell. Write down the formula that you entered into the spreadsheet.
- The electrical energy produced by a silicon solar cell cannot exceed \((1.1\text{ eV})\ \times\text{ (number of absorbed photons)}\). Calculate the maximum possible rate that electrical energy could be produced by a solar cell attached to this satellite per unit area. Give your answer in units of \(\text{W/m}^2\).
- Compare your answers to part a and part d. What is the maximum possible efficiency of the solar cell (i.e. the ratio of the electrical energy output to the total energy input)?