Contemporary Challenges: Spring-2025
Week 10 HW : Due 30 Friday

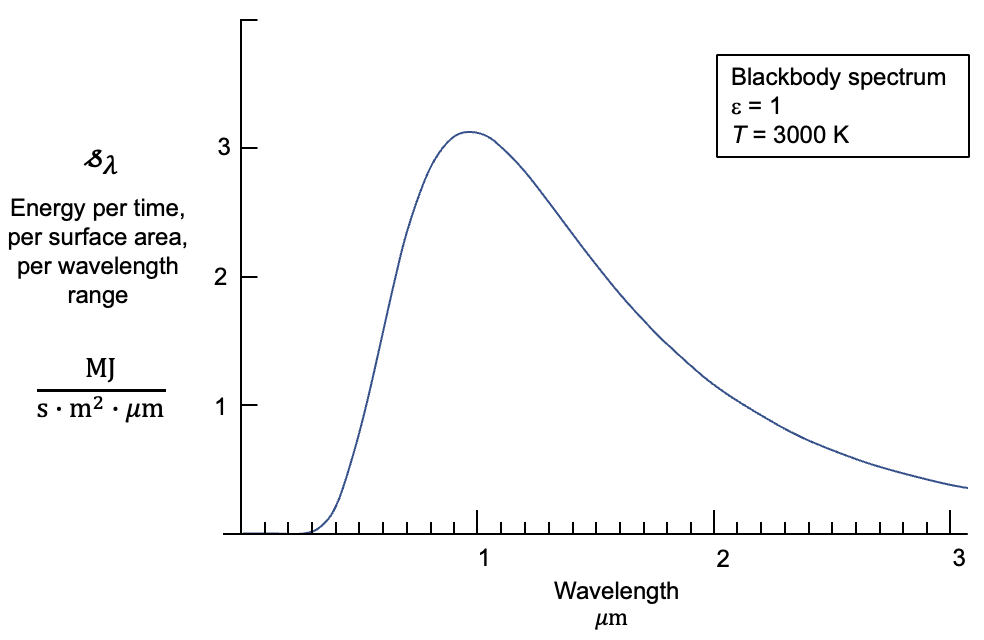
1. Approx. Integral of Planck Spectrum S0 5233S For the spectrum drawn below, estimate the integral from \(\lambda=0\) to \(\infty \) by using the height-times-width technique (you will need to estimate the full width at half maximum). Give a numerical answer with appropriate units based on the units of the x-axis and y-axis. Compare your answer to the exact value of the integral which can be quickly computed from the Stefan-Boltzman Law.
   
2. Reentry Heating of the Space Shuttle S0 5233S

   When NASA's Space Shuttle Orbiter descends from orbit it must pass through the upper reaches of Earth's atmosphere where the air is extremely thin. In this upper atmosphere, air molecules collide with the space shuttle and cause significant heating (transfer of kinetic energy). At very high altitudes, there aren't enough air molecules for convective heat transport. At these altitudes, the primary mechanism for cooling the Orbiter is the emission of blackbody radiation.

   The Orbiter has a heat shield on its underside (see the black panels in the photo at the bottom of the page). This heat shield reaches a temperature of 2000 K. The topside of the Orbiter stays cool (\(\approx\) 300 K).

   

   Estimate the maximum rate of decent of the shuttle through the upper atmosphere (the decrease in elevation per unit time). The primary constraint is that the temperature of the heat shield cannot safely exceed 2000 K (glowing red hot). This estimate will require a few steps:

   1. At what rate is blackbody radiation emitted from the Orbiter's heat shield when its underside reaches a temperature of 2000 K? Give your answer in J/s.

      Note: the space shuttle is about 35 m long, and has a wingspan (from wingtip to wingtip) of 25 m.

   2. The Orbiter has a velocity component parallel to the Earth's surface, \(v_\parallel\), and a velocity component pointing toward the Earth's surface, \(v_\perp\). To build physical intuition about the descent, let's use reasoning and simple modeling to test some hypotheses about the dominant energy transformations involved. As a first hypothesis, we'll consider a plausible coarse-grained model: assume the Orbiter's total kinetic energy remains constant during reentry, while its gravitational potential energy decreases. Apply the First Law of Thermodynamics (conservation of energy) to estimate the maximum value of \(v_\perp\). Express your answer in units of m/s.

      Note: Gravitational potential energy is changing, and electromagnetic radiation energy is being generated. The orbiter's mass is about 80,000 kg, similar to the mass of 80 cars.

   3. Now try analyzing the descent again, this time accounting for the changing kinetic energy of the Orbiter. Use the following information to construct a plausible coarse-grained model. As before, we're using physical reasoning to test hypotheses about the descent, but now incorporating additional detail to better reflect the energy transformations involved. Our goal is to estimate the time required for a safe descent:

      Time of ignition for the de-orbit burn is about 60 minutes before landing. The burn lasts 3 to 4 minutes and slows the Orbiter enough to begin its descent. About 30 minutes before landing, the Orbiter begins to encounter the effects of the upper atmosphere and the heat shields start to heat up. This usually occurs at an altitude of about 130 km, more than 8,000 km from the landing site. At this point, the Orbiter is traveling at 7500 m/s relative to the atmosphere. Around 15 minutes before landing, it has descended to an altitude of about 10 km (comparable to the cruising altitude of commercial aircraft) and is traveling at approximately the speed of sound (340 m/s).

      Using this new information about changes in velocity and altitude, estimate the time required for “braking with fire” (the hot and fiery segment of the descent). Compare to the actual timeline. What physical mechanisms are still missing from the coarse-grained model of the fiery descent? What would be a sensible next level of model refinement?

3. Infrared light interacting with gases in the atmosphere S0 5233S

   This question uses web-based software called MODTRAN which was published by Prof. David Arche (Univ. of Chicago). MODTRAN calculates how much infrared (IR) radiation leaves the Earth's atmosphere and travels away into outer space. This quantity is called “upward IR heat flux”. Open the webpage and switch the graph to wavelength. You can play with the model inputs.

   

   We will investigate the role of methane in the atmosphere. Methane has an absorption cross-section of about \(10^{-11} \ \mu\text{m}^2\) at a wavelength of about \(8\ \mu\text{m}\) (for comparison, \(\text{CO}_2\) has an absorption cross-section of about \(10^{-11}\ \mu\text{m}^2\) at \(15\ \mu\text{m}\)). The concentration of methane in our atmosphere is currently about 2 ppm.

   1. Make a pen-and-paper estimate (no computer modelling) for the optical depth of the atmosphere when light has wavelength \(8\ \mu\text{m}\) and the atmosphere contains 2 ppm methane. Assume standard temperature and pressure, and a methane absorption cross section of \(10^{-11} \ \mu\text{m}^2\) . Give your answer in meters.
   2. Use the computer model to remove all greenhouse gases from the atmosphere except for methane. Set methane to 2 ppm. Then try increasing methane to 4 ppm. What is the change in the “upward IR heat flux” when you change from from 2 to 4 ppm?
   3. Now we will check what happens when the \(\text{CO}_2\) concentration is increased by 2 ppm. Use the computer model to remove all greenhouse gases from the atmosphere except for \(\text{CO}_2\) (set \(\text{CO}_2\) to 410 ppm). Increase the \(\text{CO}_2\) concentration to 412 ppm. What is the change in the “upward IR heat flux”? (The online user interface might not show you enough significant figures. If this is the case, increase \(\text{CO}_2\) from 410 to 430 ppm and then do a linear interpolation to estimate the change between 410 and 412 ppm).
   4. Try to explain the results of part b and c to a non-scientist. You may want to use the concepts of “optical depth” and “saturating an absorption dip”.

   For additional information about greenhouse gases, I recommend the highly accessible/readable Chapter 4 from Prof. Archer's textbook "Global Warming: Understanding the Forecast".

4. Two-layer model for estimating the Earth’s temperature S0 5233S
   

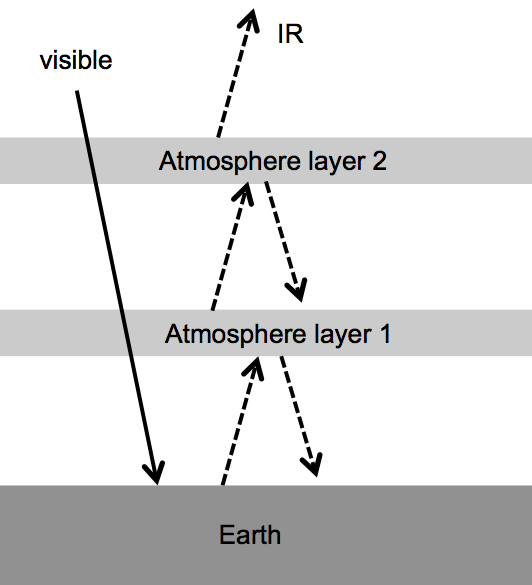
   The Figure shows a two-layer model of the Earth's atmosphere. Both atmospheric layers are transparent to visible light, but fully absorb infra-red (IR) light. The atmospheric layers absorb, thermalize and re-emit infrared radiation. The temperature of each layer is stable, meaning that “power in“ is equal to “power out“ for each layer.

   1. Write down three equations that represent the balance of power for the three objects in this model (the ground, layer 1 and layer 2). Write a fourth equation that represents the balance of power for the combined system (earth + atmosphere) which is receiving solar energy and radiating IR into outerspace. Give your answers as symbolic expressions.
   2. Find the temperature of the earth's surface when the intensity of incoming sunlight is 1360 J/(s.m²). Note that 30% of this sunlight is reflected immediately back into outerspace.

   3. Optional, not graded Find the upward IR flux that is emitted into outer space as a function of the ground temperature. Give you answer as a symbolic expression.

   4. Optional, not graded Calculate the upward IR flux when the ground temperature is 300 K.