Contemporary Challenges: Spring-2025
Homework 3 : Due 9 Friday
- Hot showers and standard deviation
S0 5224S
(a) Estimate the energy used during a typical 10-minute shower in the United States. The dominant variables in this problem are the temperature rise of the water and the flow rate of the showerhead. Develop a coarse-grained model that incorporates these two variables. For simplicity, you may assume: (i) The water heater is 100% efficient at converting electrical energy into heat, and (ii) the water heater is located close to the shower, so heat losses in the pipes can be neglected.

(b) Develop a reasonable estimate for the standard deviation of your answer to part a. That is, imagine measuring the energy used for a 10-minute shower in a thousand randomly selected U.S. households. How much would the energy use vary? To develop a reasonable estimate, spend a little time doing internet research (or in-person research) on the variability of shower flow rates, the variability of ground temperature, and the variability of shower water temperature (personal preference). Once you can justify reasonable numbers for the variability of these inputs, propogate the uncertainty through your coarse-grained model using the methods we discussed in class.
(c) Sense making: Compare the typical energy used for a 10-minute shower to the typical energy used to drive an elecric car at 70 mph for 10 minutes.
- Gasoline Sun
S0 5224S
Electromagnetic radiation energy from the Sun arrives at the upper atmosphere of our planet at a rate of about 1350 J/(s \(\cdot\) m\(^2\)). Use this information, together with the average radius of the Earth's orbit, to show that the Sun radiates energy at a rate of about \(4 \times 10^{26}\) J/s.
We know from radiometric dating of rocks on Earth (and the Moon and Mars) that our solar system is about 4 billion years old. Let's make a naïve hypothesis (like scientists did in the early 1900s) that the Sun is powered by burning hydrocarbons. What mass of gasoline would be needed to power the Sun at a rate of \(4 \times 10^{26}\) J/s for 4 billion years? Compare to the actual mass of the Sun.
Note: The energy density of hydrocarbon fuels, including gasoline, natural gas, dry logs of wood, chocolate, croissants, gummy bears, etc. etc. is \(\approx\) 40 MJ/kg.
- Practice Nuclear Physics
S0 5224S
1. Rutherford scattering
Based on Q13M.2 from Unit Q 3rd Edition
Estimate the minimum kinetic energy that an alpha particle must have to get stuck to a gold nucleus? Give your answer in both joules and electron volts.(Note: The atomic number of gold is \(Z = 79\), the mass number of gold is \(A = 197\). An alpha particle consists of 2 protons and 2 neutrons. This question can be solved using knowledge of the Coulomb potential for a system of two point charges).
-
2. Fusion
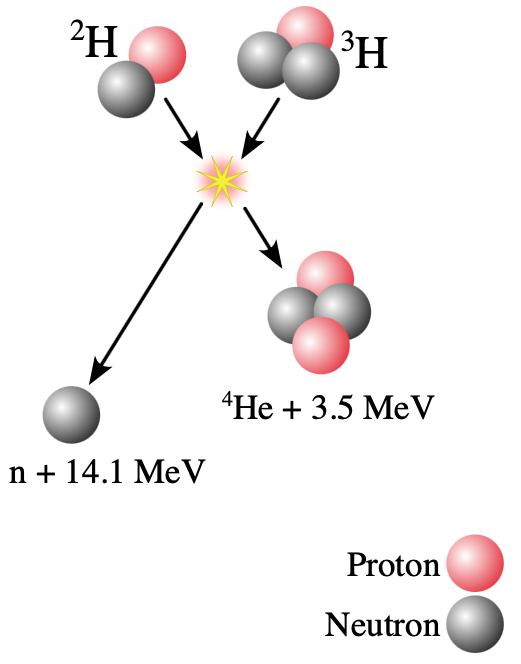
- The figure shows the fusion reaction between tritium and deuterium. How much electrostatic potential energy will tritium and deuterium have just before the strong force overwhelms the electrostatic repulsion and sticks them together? You can assume that tritium and deuterium start to attract each other via the strong force when the center-to-center distance is about 10 fm.
- Fusion is happening in a gas of tritium and deuterium. Estimate the temperature of the gas. Give your answer in kelvin. (Use the equipartition theorem to help you solve this: the average kinetic energy of a gas atom is \((3/2)k_BT\), where \(k_B\) is the Boltzmann constant).
- Three ideas for the term project
S0 5224S
Read the description of the term project on the class website at “Introduction to term project”. Identify three (3) subjects that you find interesting/intriguing (for example, solar energy, exoplanets, ...). Within each subject, pose a question that might have an interesting quantitative answer: “Since it requires energy to make a solar panel, how long does it take to recoup that energy?”, “How far away could we see an Earth-like planet orbiting a Sun-like star?” ... You should turn in 3 different subjects and 3 different quantitative questions (quantitative means “quantities that can be calculated and/or measured”)
Let your mind wander as broadly as possible. Subjects and questions are not restricted to the topics taught in PH315. During this exploratory stage, be bold and daring; you are not committing yourself to solve all 3 questions. To spark your imagination, there is a list of ideas on the class website. The instructor will read your ideas and give you feedback. Whenever possible, the feedback will point you towards a coarse-grained model that is helpful for answering your question. Use the feedback to help decide which question you will develop further (or whether you need to go back to the drawing board).