Contemporary Challenges: Fall-2023
Nuclear Physics Practice Problems (SOLUTION): Due 30 Wednesday
- Practice Nuclear Physics
S1 4749S
1. Rutherford scattering
Based on Q13M.2 from Unit Q 3rd Edition
Estimate the minimum kinetic energy that an alpha particle must have to get stuck to a gold nucleus? Give your answer in both joules and electron volts.(Note: The atomic number of gold is \(Z = 79\), the mass number of gold is \(A = 197\). An alpha particle consists of 2 protons and 2 neutrons. This question can be solved using knowledge of the Coulomb potential for a system of two point charges).
An alpha particle can get inside a gold nucleus if its initial kinetic energy is large enough to overcome the electrostatic repulsion between the positively charged gold nucleus and the positively charged alpha particle. We need to calculate the electrostatic potential energy when the surface of an alpha particle is about to touch the surface of a gold nucleus. The nuclear radius of gold is estimated from \(r_{\text{Au}}=r_{0} A^{1 / 3}=7.27\ \mathrm{fm}\) where \(A=197\) is the mass number and \(r_0 = 1.2 \text{ fm}\). The nuclear radius of the alpha particle is estimate by \(r_{\text{alpha}}=r_{0} 4^{1 / 3}=1.9\ \mathrm{fm}\). Therefore, the kinetic energy that the alpha particle needs is \begin{align} KE_{\alpha}&=k \cdot \frac{2 e \cdot 79 e}{ r_{\text{Au}}+r_{\text{alpha}}}\\ &=4 \times 10^{-12} \text{ J}\\ &=25\text{ MeV} \end{align}
where \(k\) is the Coulomb's law constant \(9 \times 10^9\) J.m/C\(^2\).
-
2. Fusion
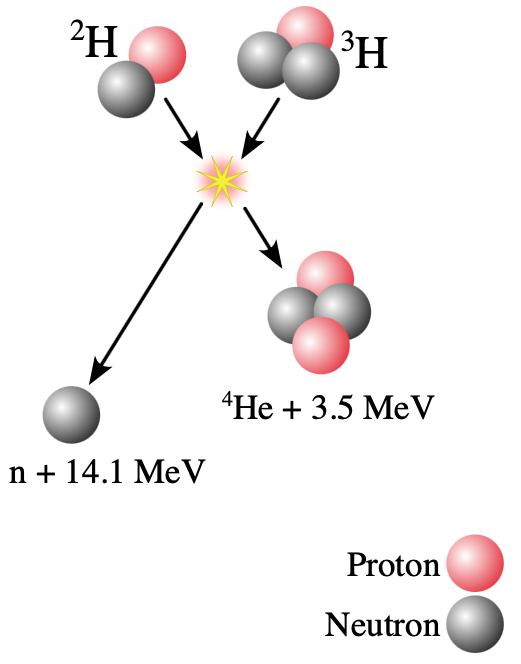
- The figure shows the fusion reaction between tritium and deuterium. How much electrostatic potential energy will tritium and deuterium have just before the strong force overwhelms the electrostatic repulsion and sticks them together? You can assume that tritium and deuterium start to attract each other via the strong force when the center-to-center distance is about 10 fm.
- Fusion is happening in a gas of tritium and deuterium. Estimate the temperature of the gas. Give your answer in kelvin. (Use the equipartition theorem to help you solve this: the average kinetic energy of a gas atom is \((3/2)k_BT\), where \(k_B\) is the Boltzmann constant).
- \(U_{electric}=k \cdot \frac{e^2}{ [10^{-14} \text{ m}]}= 2.3 \times 10^{-14} \text{ J}\).
- From equipartition theorem, we expect each particle in the gas to have kinetic energy \begin{align} KE \approx (3/2)k_BT\\ \end{align} We want the tritium and deuterium to each have \(KE \approx 1.15 \times 10^{-14} \text{ J}\), so that their combined kinetic energy is \(2.3 \times 10^{-14} \text{ J}\). (This combined kinetic energy is also called the center-of-mass kinetic energy of a two-particle system). \begin{align} T &= (2/3) \frac{1.15 \times 10^{-14} \text{ J}}{3k_B}\\ &= \frac{2.3 \times 10^{-14} \text{ J}}{3\cdot 1.38 \times 10^{-23} \text{ J/K}}\\ &= 5.5\times 10^{8} \text{ K}\\ &= 550 \text{ million K} \end{align}
- Compare the mass of \(^3\)He (a nucleus with two protons and one neutron) to the combined mass of two isolated protons and one isolated neutron. Rather than look up emperical measurements, try estimating the mass difference using a coarse-grained model. Utilize the model mentioned in class (the biggest contributions to binding energy are the electrostatic interaction and the strong interaction, with every contact point between adjacent nucleons contributing about 3 MeV to the strong interaction term). Estimate the mass difference and give your answer in kilograms. State which mass is greater.