Central Forces: Spring-2025
HW 04: Due W2 D5

  1. Sun vs. Jupiter

    Gain experience with the relative sizes of objects and distances in the Solar System. Gain experience with realistic reduced masses.

    Calculate the following quantities:

    1. Find \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) and \(\mu\) for the Sun-Earth system. Compare \(|{\vec r}_{\rm sun}-{\vec r}_{\rm cm}|\) to the radius of the Sun and to the distance from the Sun to the Earth. Compare \(\mu\) to the mass of the Sun and the mass of the Earth.
    2. Repeat the calculation for the Sun-Jupiter system.

  2. Undo Formulas for Center of Mass (Geometry)

    (Sketch limiting cases) Purpose: For two central force systems that share the same reduced mass system, discover how the motions of the original systems are the same and different.

    The figure below shows the position vector \(\vec r\) and the orbit of a “fictitious” reduced mass \(\mu\).

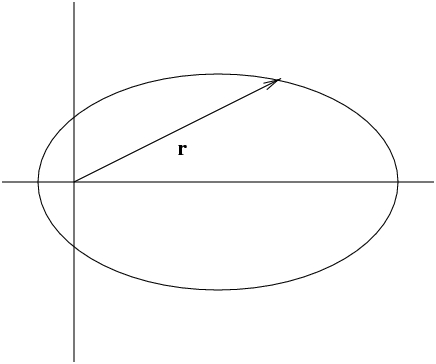
    1. Suppose \(m_1=m_2\), Sketch the position vectors and orbits for \(m_1\) and \(m_2\) corresponding to \(\vec{r}\). Describe a common physics example of central force motion for which \(m_1=m_2\).
    2. Repeat, for \(m_2>m_1\).

  3. Angular Momentum and Kinetic Energy in the Center of Mass

    (Messy algebra) Convince yourself that the expressions for kinetic energy in original and center of mass coordinates are equivalent. The same for angular momentum.

    Consider a system of two particles of mass \(m_1\) and \(m_2\).

    1. Show that the total kinetic energy of the system is the same as that of two “fictitious” particles: one of mass \(M=m_1+m_2\) moving with the velocity of the center of mass and one of mass \(\mu\) (the reduced mass) moving with the velocity of the relative position.
    2. Show that the total angular momentum of the system can similarly be decomposed into the angular momenta of these two fictitious particles.

  4. Confidence Rating After solving each problem on the assignment, indicate your answers to the following questions for each problem. Answer for the problem as a whole, even if the problem has multiple parts.
    1. Question Confidence How confident are you that you are interpreting the problem the way the instructor intends?

      For the rest of the questions, assume you have interpreted the problem correctly
    2. Problem Confidence How confident are you that you could independently come up with a correct solution process to a similar problem on a future problem set?
    3. Answer Confidence How confident are you that your final answer to this question is correct (not solution process)?
    4. Makes Sense To what degree do you understand how your answer fits (or does not fit) the physical or mathematical situation of the problem?