Quantum Fundamentals: Winter-2026
HW3: Due W2 D3
- Eigenvectors of the Rotation Matrix
The orthogonal matrix
\[R_z(\theta)=
\begin{pmatrix}
\cos\theta&-\sin\theta&0\\ \sin\theta&\cos\theta&0\\ 0&0&1\\
\end{pmatrix}
\]
corresponds to a rotation around the \(z\)-axis by the angle \(\theta\).
- Find the eigenvalues of this matrix.
- Find the normalized eigenvectors of this matrix.
- Describe how the eigenvectors do or do not correspond to the vectors which are held constant or “only stretched” by this transformation.
- Stern Gerlach Explain
Use words and equations to explain the key features of the Stern-Gerlach experiment.
Contrast Classical/Quantum Explain what you would predict based only on classical physics for the Stern-Gerlach experiment and describe the difference between the classical prediction and the actual experimental results.
- Statistical Analysis of the Spins Sim
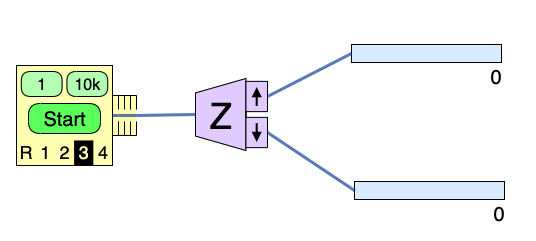
In the spins sim, the oven can be set to emit particles in a particular unknown prepared state (instead of in a random state).
- Set the oven to Unknown #3.
- Orient the analyzer in the \(z\)-direction.
- Perform 5 sets of 10,000 Stern-Gerlach experiments (10,000 particles are sent through a Stern-Gerlach Analyzer) and record the number of particles that end up in the top counter.
- For each set of experiments, calculate the probability that a single particle was measured to have \(S_z = +\hbar/2\).
Do all of the following calculations by hand (you can use a calculator to help with the arithmetic).
Plot a histogram of the probabilities you measured for each set. Use a bin size of 0.002 for the horizontal axis. (Choose appropriate values on the horizontal axis. You don't need to plot the full possible values 0-1. You may use a computer to make the histogram or you can sketch it by hand.)
- What is your best estimate of the probability that, when you measure \(S_z\) of a particle in the Unknown #3 state, you will get a result of \(+\hbar/2\)? Mark this value on your histogram.