Quantum Fundamentals: Winter-2026
HW 6: Due W3 D5
- Measurement Probabilities (Brief)
A beam of spin-\(\frac{1}{2}\) particles is prepared in the initial state \[ \left\vert \psi\right\rangle = \sqrt{\frac{2}{5}}\; |+\rangle_x - \sqrt{\frac{3}{5}}\; |-\rangle_x \](Note: this state is written in the \(S_x\) basis!)
- What are the possible measurement values if you measure the spin component \(S_x\), and with what probabilities would they occur?
- What are the possible measurement values if you measure the spin component \(S_z\), and with what probabilities would they occur?
- Completeness Relation Change of Basis
Given the polar basis kets written as a superposition of Cartesian kets \begin{eqnarray*} \left|{\hat{s}}\right\rangle &=& \cos\phi \left|{\hat{x}}\right\rangle + \sin\phi \left|{\hat{y}}\right\rangle \\ \left|{\hat{\phi}}\right\rangle &=& -\sin\phi \left|{\hat{x}}\right\rangle + \cos\phi \left|{\hat{y}}\right\rangle \end{eqnarray*}
Find the following quantities: \[\left\langle {\hat{x}}\middle|{\hat{s}}\right\rangle ,\quad \left\langle {\hat{y}}\middle|{{\hat{s}}}\right\rangle ,\quad \left\langle {\hat{x}}\middle|{\hat{\phi}}\right\rangle ,\quad \left\langle {\hat{y}}\middle|{\hat{\phi}}\right\rangle \]
- Given a vector written in the polar basis
\[\left|{\vec{v}}\right\rangle = a\left|{\hat{s}}\right\rangle + b\left|{\hat{\phi}}\right\rangle \]
where \(a\) and \(b\) are known.
Express \(\left|{\vec{v}}\right\rangle \) in the Cartesian basis, \[\left|{\vec{v}}\right\rangle = c\left|{\hat{x}}\right\rangle + d\left|{\hat{y}}\right\rangle \] by finding \(c\) and \(d\)
Hint: Use the completeness relation: \(\left|{\hat{x}}\right\rangle \left\langle {\hat{x}}\right| + \left|{\hat{y}}\right\rangle \left\langle {\hat{y}}\right| = 1\) - Given a quantum state written in the \(S_z\) basis, \[ \left|{\Psi}\right\rangle = g \left|{+}\right\rangle + h \left|{-}\right\rangle , \] express \(\left|{\Psi}\right\rangle \) in the \(S_y\) basis. That is, find coefficients \(j\) and \(k\) such that \[ \left|{\Psi}\right\rangle = j \left|{+}\right\rangle _y + k \left|{-}\right\rangle _y. \]
- Spin One Intro
The OSP Spins Laboratory simulation can also be used to explore spin-1 systems. The components of spin for these systems can be measured to be:
\(\hbar\) (corresponding to the “+” port)
\(0\hbar\) (corresponding to the “0” port)
\(-\hbar\) (corresponding to the “-” port)
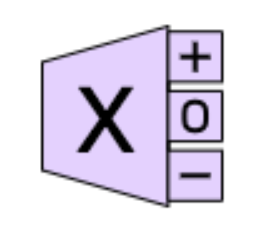
To switch the simulation to a spin-1 system, find the hyperlink about halfway down the page that says “Click here to switch”.
Draw and label a diagram of an experimental setup that would allow you to prepare a set of spin-1 particles to be in the \(|1\rangle_x\) state and than measure the \(z\) component of spin for these particles.
- Using the simulation, prepare a set of particles to be in the \(|1\rangle_x\) state and measure the \(x\), \(y\), and \(z\) components of spin of these particles. Draw probability histograms of the results for each spin-component-direction \(S_x\), \(S_y\), and \(S_z\).