Quantum Fundamentals: Winter-2026
HW 5: Due W3 D3
- Chained Stern-Gerlach (Brief)
Consider the Stern-Gerlach set-up shown, with a thermal oven source, and some state vectors associated with various analyzer outputs:
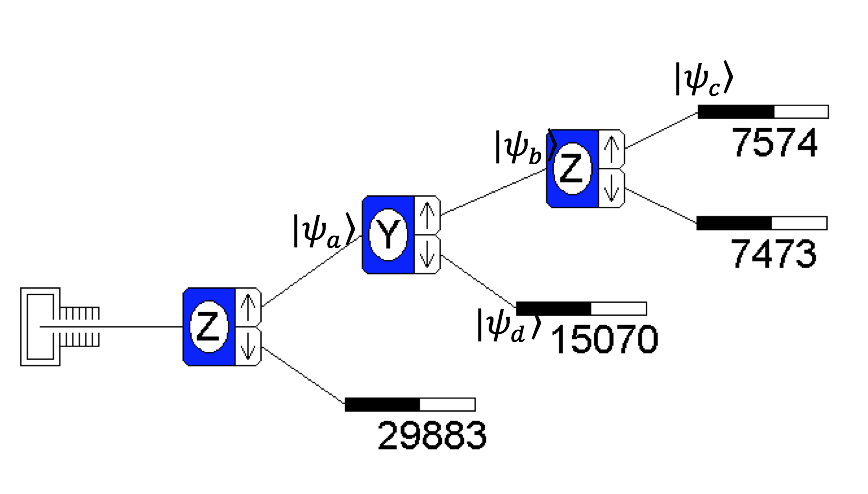
How many particles were released from the oven?
- Write down Dirac notation expressions for \(|\Psi_a\rangle\), \(|\Psi_b\rangle\), \(|\Psi_c\rangle\), and \(|\Psi_d\rangle\) in the \(S_z\) basis (i.e., as linear superpositions of \(|+\rangle_z\) and \(|-\rangle_z\)).
- Spin One Half Unknowns (Brief)
Using the SPINS simulation for a spin-\(\tfrac{1}{2}\) system
(Spins simulation),
for the unknown initial state \(\left|{\psi_4}\right\rangle \), perform measurements of
\(S_x\), \(S_y\), and \(S_z\) separately, and for each measurement determine the probability of obtaining each possible measurement value.(We carried out the same procedure for \(\left|{\psi_3}\right\rangle \) in class; you may
refer to that example.)
- Use the probabilities you observed from the measurements to express \(\left|{\psi_4}\right\rangle \) as a linear superposition of the \(S_z\)-basis states \(\left|{+}\right\rangle \) and \(\left|{-}\right\rangle \).
- Articulate a Process: Write a set of general instructions that would allow another student in next year's class to find an unknown state from probabilities obtained from spin measurements.
- Compare Theory with Experiment: Design an experiment that will allow you to test whether the state you identified in Question (a) for the unknown state \(\left|{\psi_4}\right\rangle \) is correct. Describe your experiment here, clearly but succinctly, as if you were writing it up for a paper. Do the experiment and discuss your results.
- Make a Conceptual Connection: In general, are the probabilities obtained from spin-component measurements along only two spin directions (for example, the \(z\) direction and the \(y\) direction) sufficient to determine a spin-\(\tfrac{1}{2}\) quantum state? Why or why not?
- Spin Calculations (brief)
A set of spin-1/2 particles are identically prepared in the state \[\left|{\psi_A}\right\rangle =N\bigg(\sqrt{3}\left|{+}\right\rangle +e^{i\pi/3}\left|{-}\right\rangle \bigg)\] .
Determine \(N\) so that the state is normalized.
What values of the z-component of spin might you measure and with what probabilities?
What values of the y-component of spin might you measure and with what probabilities?
Write this state in the \(S_x\) basis (i.e., as a linear superposition of \(|+\rangle_x\) and \(|-\rangle_x\)).
In what direction would you have to orient a Stern-Gerlach analyzer so that ALL the particles prepared in the state \(\left|{\psi_A}\right\rangle \) would be measured to have a spin component in that direction equal to \(+\hbar/2\)? Give the direction in spherical coordinates, \(\theta\) and \(\phi\).