Quantum Fundamentals: Winter-2026
HW 2: Due W1 D5 MathBits
- Commutator of Linear Transformations
Consider the following matrices:
\[A=
\begin{pmatrix}
0&1\\ 1&0\\
\end{pmatrix}\qquad
B=
\begin{pmatrix}
3&1\\ 1&3\\
\end{pmatrix}\qquad
C=
\begin{pmatrix}
1&0\\ 0&-1\\
\end{pmatrix}
\]
- Explain what each of the matrices “does” geometrically when thought of as a linear transformation acting on a vector.
- The commutator of two matrices \(A\) and \(B\) is defined by \(\left[A, B\right]\buildrel \rm def \over = AB-BA\). Find the following commutators: \(\left[A,B\right]\), \(\left[A,C\right]\), \(\left[B,C\right]\). Two matrices are said to commute, if their commutator is zero.
- Thought of as linear transformations, two matrices commute if it doesn't matter in which order the transformations act. For all pairs of the matrices \(A\), \(B\), and \(C\), discuss geometrically that the order of the transformations doesn't matter for the transformations that commute, but that the order does matter when the transformations don't commute.
- Finding Orthogonal Vectors (Brief Version)
Consider the quantum state: \[\left\vert \psi\right\rangle = \frac{1}{\sqrt{3}}\left\vert +\right\rangle+ i\frac{\sqrt{2}}{\sqrt{3}} \left\vert -\right\rangle\]
Find the normalized vector \(\vert \phi\rangle\) that is orthogonal to it.
- Graphs of the Complex Conjugate
For each of the following complex numbers, determine the complex conjugate, square, and norm. Then, plot and clearly label each \(z\), \(z^*\), and \(|z|\) on an Argand diagram.
- \(z_1=4i-3\)
- \(z_2=5e^{-i\pi/3}\)
- \(z_3=-8\)
- In a few full sentences, explain the geometric meaning of the complex conjugate and norm.
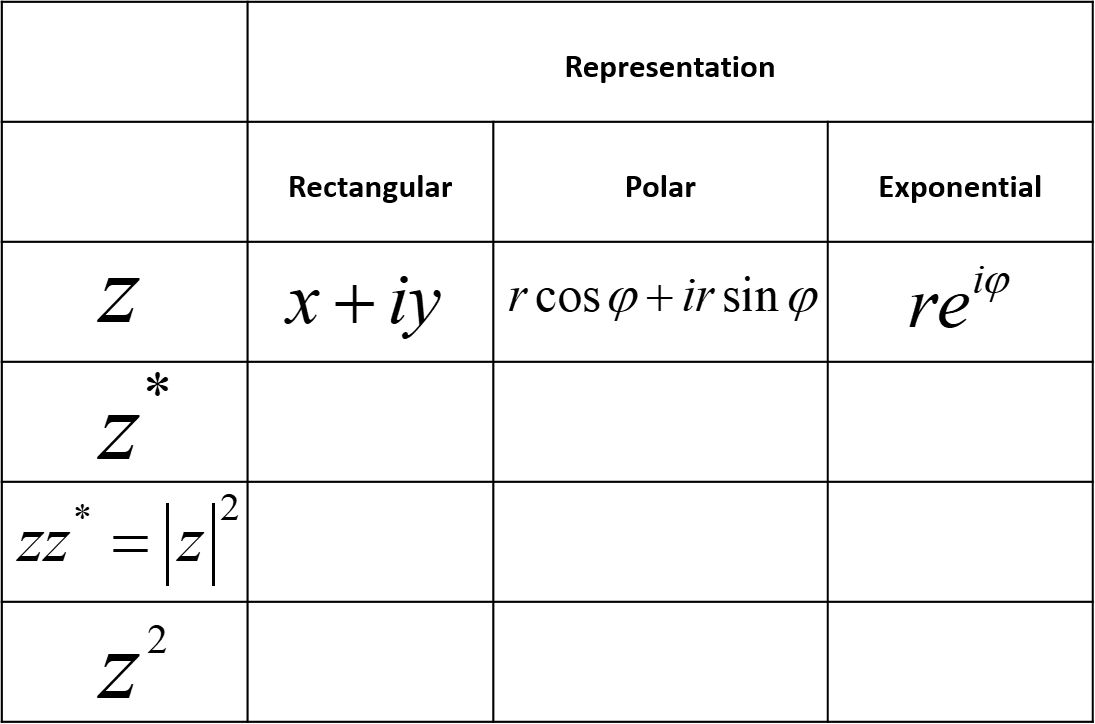
- Representations of Complex Numbers--Table
Fill out the table above that asks you to do several simple complex number calculations in rectangular, polar, and exponential representations.