Oscillations and Waves: Spring-2025
HW 4b: Due W4 D5
- Interpreting Parameters of Waves
\[\psi(x,t)=A\cos{(-kx+\omega t+\phi)}\] for \(A=1\) unit; \(k=2\pi\,m^{-1}\); \(\omega=\pi\,rad/s\). What is the wavelength, period, amplitude of the disturbance (don't forget units)? Discuss the dimensions of \(A\). What value of \(\phi\) makes \(\psi(x,t)=0\) at the origin at \(t=0\)?
Plot in Mathematica (or similar) two spatial cycles of the waveform and animate for two time periods.
Which direction does the wave travel and with what speed? Which direction does it travel if you change the sign of the position term? Of the time term? Of both? Why?
- Focus on the position \(x = 0\,m\). At what rate is the quantity represented by \(y\) changing? (This is called the “material” velocity). Describe the variation of this quantity over one cycle. Is it constant? Or does it change? Can it be positive or negative?
- Forms of Wave Functions
Write down a sinusoidal waveform \(\psi(x, t)\) that has the following properties:
Amplitude \(2\,m\), wavelength \(10\,m\), travels to the right at \(1\,\frac{m}{s}\), \(\psi=2\,m\) at \(x=5\,m\) and \(t=0\,s\).
- Standing wave, amplitude \(5\,m\), period \(1\,s\), wavelength \(1\,m\) that is momentaily flat at \(t=0\,s\).
- Solutions to the Wave Equation
Describe the following waveforms in words (waveform, period, phase angel, direction, & speed of travel, etc.)
Demonstrate whether they are, or are not, solutions to the non-dispersive wave equation: \(\frac{\partial^2}{\partial t^2}\psi(x,t)=v^2\frac{\partial^2}{\partial x^2}\psi(x,t)\).
\(\psi(x,t)=4\cos{(4\pi x+3\pi t)}-4\sin{(4\pi x +3\pi t)}\)
- \(\psi(x,t)=3\cos{(2\pi x)}\sin{(\pi t)}\)
- Non-dispersive Triangle Wave
A banjo string (mass per unit length \(\mu\) under tension \(T\)) is anchored at \(x=0\) and \(x=L\). It is displaced so that it has the following profile at \(t=0\), and the transverse velocity at all points is zero at \(t=0\). (The diagram shows a vastly exaggerated displacement -- we assume that \(A<<L\) so that the string stretches only a little and its stretched length is only slightly larger than \(L\).)
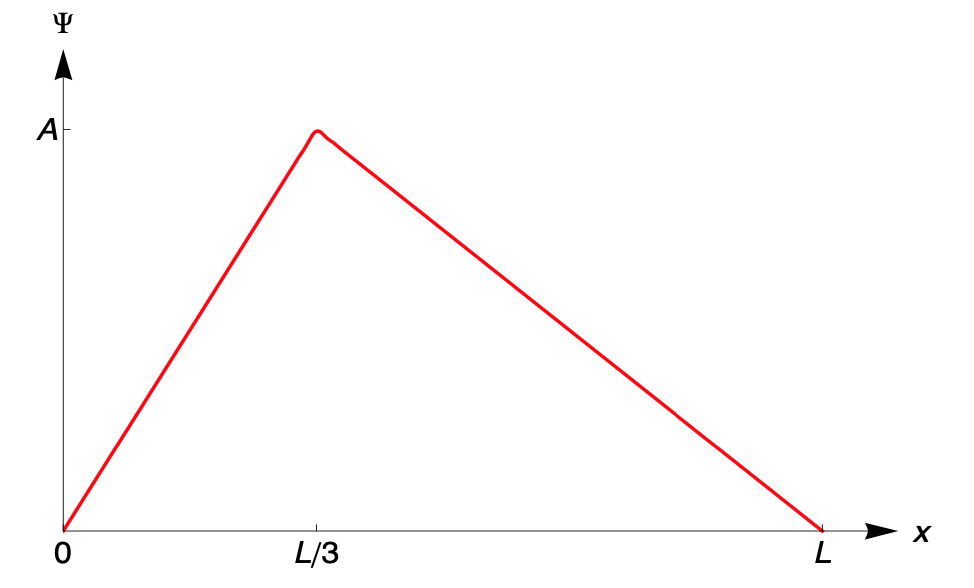
Write the wave form as a superposition of standing waves of all \(k\) values (and corresponding frequencies \(\omega_k=vk\)).
The information about the initial condition on the velocity eliminates a large number of coefficients. Which ones are zero and why?
The condition that the string is anchored at \(x=0\) eliminates more coefficients. Which ones are zero and why?
The condition that the string is anchored at \(x=L\) defines special values of \(k\) that are allowed in the sum. Define these special values \(k_n\) in terms of \(L\) and an integer variable \(n\). Rewrite the sum with all this information so that is is now a Fourier sum.
Use Fourier analysis to find the coefficients for this triangle wave at \(t=0\).
Now write the full \(\psi(x,t)\) making sure you connect the frequency in each term to the \(k\) value in each term. \[\psi(x,t)=\sum_nC_n\sin{(k_nx)}\cos{(\omega_nt)}\]
Animate the function! Does it do what you expect?
- Here we have use \(L/3\) for the peak of the wave. How would the sound of the banjo change if it was at L/2? Or L/9?