Oscillations and Waves: Spring-2025
HW 2b: Due W2 D5
- A Physical System that Oscillates
A mass \(m\) is strung on a very light wire equidistant between two anchor points separated by a distance \(2L\). When the mass is displaced laterally (i.e. plucked) in the \(x\)-direction (here vertically), there is constant tension \(T\) on the wire that produces a restoring force.
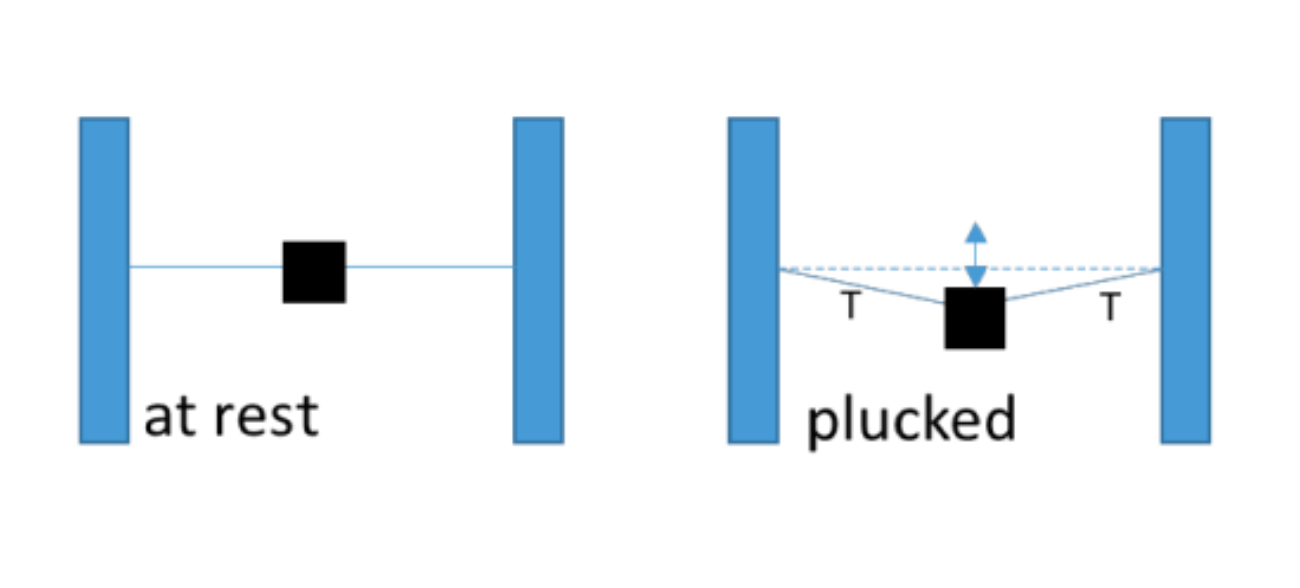
What is the resulting natural frequency \(\omega_0\) of the oscillating mass? Assume tension drives the oscillation (i.e. no gravity) and assume the angle the string makes with the posts is small.
Note: \(\omega_0\) must be expressed in terms of the physical parameters given in the problem (\(T, L, m\)).
- Write a generic expression for displacement from equilibrium in any of the standard forms, \(ABCD\).
- Phase lead/lag
- Sketch on one plot, two oscillations (\(\#1\) and \(\#2\)) of the same period (\(1\,s\)), where oscillation \(\#2\) has an amplitude that is twice that of oscillation \(\#1\) and lags oscillation \(\#1\) by \(\frac{\pi}{4}\).
Sketch on one plot, the charge \[q(t) = Q \cos{(\omega_0 t)}\] and the current \[I(t) = \dot{q}(t)\] and say which one leads and by what phase. Give a verbal explanation.
Note: It is good to object to plotting \(2\) quantities with different dimensions on the same vertical axis! But it is okay if you think of the plot as having a left vertical axis for one quantity and a right axis for the other. The important thing is to get the horizontal time axis to line up for both oscillations.
- Damped Oscillator
An undamped oscillator has a period \(T_1=1.000\) s, that increases to \(T_2=1.001\) s when damping is added.
What is the damping factor \(\beta\)?
- By what factor does the oscillation amplitude decrease after 10 cycles?
- Underdamped LRC Oscillator
Consider an oscillator with capacitance \(C=18\,nF=18\times 10^{-9}\,F\), a resistor of resistance \(R=50\,\Omega\) and an inductor with an inductance \(L=22\,mH=0.022\,H\). Charge the isolated capacitor up and then connect it in series to the \(L\) and \(R\) and allow it to discharge. Assume the starting time is \(t=0\).
What are the initial conditions for this circuit?
What is the damping time (time for amplitude to decay to \(1/e\) of starting value)?
By what fraction is the oscillation frequency shifted from the undamped version?
How many cycles occur within the damping time?
What is the value of the quality factor (or Q-factor) of the circuit? Look up another system to put this Q-factor in some sort of context.
How long will it take for the system lose \(90\%\) of its energy?
- Plot the charge, current, and current derivative (\(\dot{I}\)) in the circuit as functions of time for enough cycles to show the damping. Use Mathematica, Python, or the software of your choice.