Oscillations and Waves: Spring-2025
HW 1b: Due W1 D5

1. Fourier Series of a Triangle Wave

   Consider the following triangle wave:

   

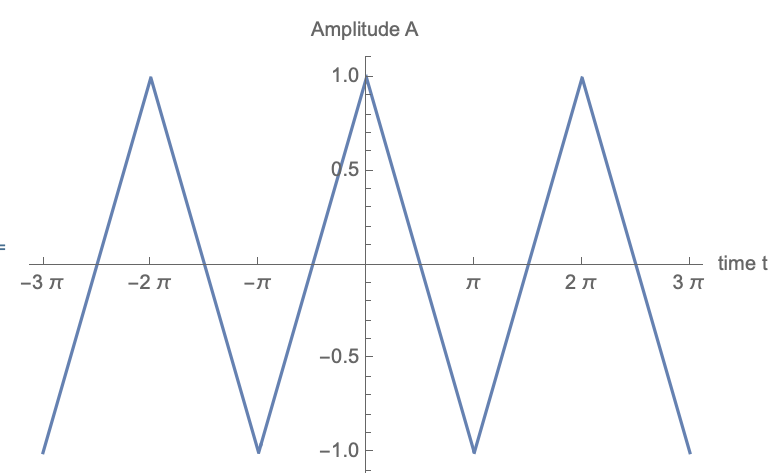
   1. Find the Fourier series for a triangle wave (such as the one shown in the figure), which has amplitude \(A\) and period \(T\).
   2. Plot several approximations to your solution including the first nonzero term and the first four nonzero terms.
   3. Make a histogram of your coefficients, i.e. find the spectrum.

2. Fourier Series for the Ground State of a Particle-in-a-Box. Treat the ground state of a quantum particle-in-a-box as a periodic function.

   1. Set up the integrals for the Fourier series for this state.

   2. Which terms will have the largest coefficients? Explain briefly.

   3. Are there any coefficients that you know will be zero? Explain briefly.

   4. Using the technology of your choice or by hand, calculate the four largest coefficients. With screen shots or otherwise, show your work.

   5. Using the technology of your choice, plot the ground state and your approximation on the same axes.