Theoretical Mechanics: Fall-2021
Curvilinear Coordinates Practice: Due Day 16
- Speed Squared in Curvilinear Coordinates
Show that the speed squared written in different standard coordinates systems is:
- in rectangular coordinates: \(v^2 = \dot{x}^2 + \dot{y}^2+\dot{z}^2\)
- in cylindrical coordinates: \(v^2 = \dot{s}^2 + s^2\dot{\phi}^2+\dot{z}^2\)
- in spherical coordinates: \(v^2 = \dot{r}^2 + r^2\dot{\theta}^2+r^2\sin^2\theta\dot{\phi}^2\)
where:
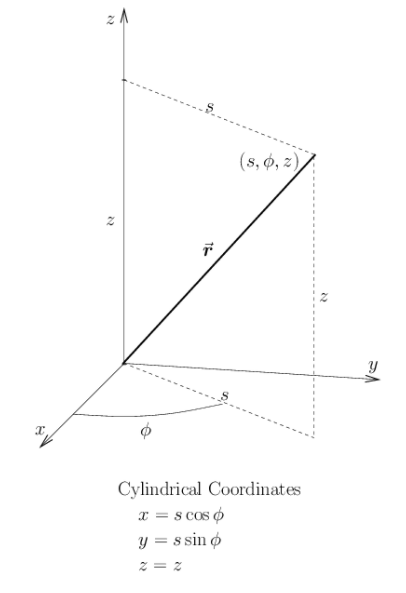
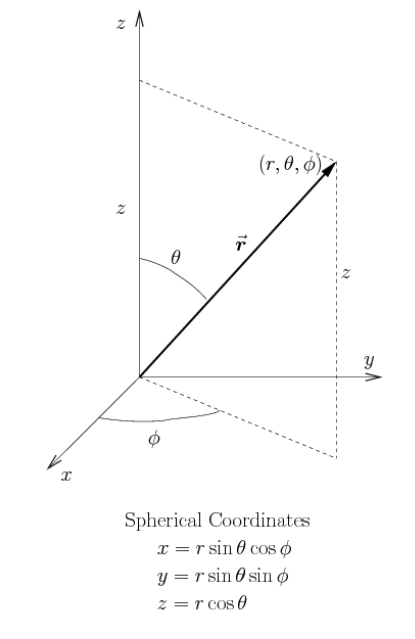
See: GVC 3.1 for more discussion of curvilinear coordinates. Note that the labels for the aximuthal and polar coordinates in different for math and physics (\(\phi\) and \(\theta\) are swapped.)
Note: For (b) and (c) You can take two different approaches:
- start with the answer to (a), calculate \(\dot{x}\) \(\dot{y}\), and \(\dot{z}\), square and plug in, or
- Write the position vector in curvilinear coordinates, differentiate (including the basis vectors!), and take the dot product of the velocity with itself.
Both of these approaches are tedious calculations, but it's good to do them once in your career to convince yourself that these expressions are true.