Problem-Solving: Fall-2024
Tutorial 2 (Required): Due W2 D2
- Tetrahedron
Using a dot product, find the angle between any two line segments that join the center of a regular tetrahedron to its vertices. Hint: Think of the vertices of the tetrahedron as sitting at the vertices of a cube (at coordinates (0,0,0), (1,1,0), (1,0,1) and (0,1,1)---you may need to build a model and play with it to see how this works!)
- Distance Formula in Curvilinear Coordinates
The distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\) and the point \(\vec r'\) is a coordinate-independent, physical and geometric quantity. But, in practice, you will need to know how to express this quantity in different coordinate systems.
Hint: Be sure to use the textbook: https://books.physics.oregonstate.edu/GSF/coords2.html
Find the distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\) and the point \(\vec r'\) in rectangular coordinates.
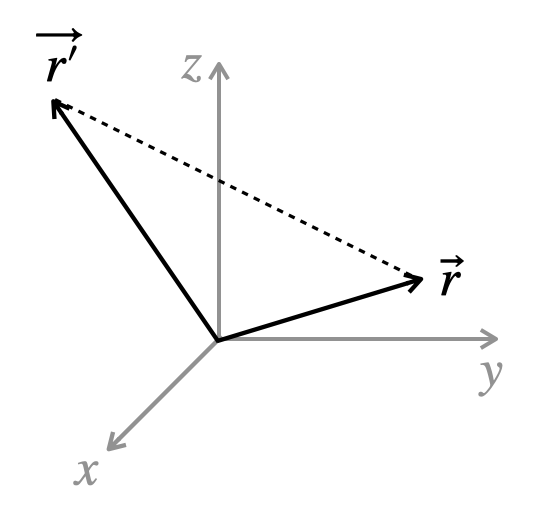
- The distance \(\left\vert\vec r -\vec r\,{}'\right\vert\) between the point \(\vec r\,{}'=(x\,{}',y\,{}',z\,{}')\) and the point \(\vec r=(x,y,z)\) is a coordinate-independent, physical and geometric quantity. But, in practice, you will need to know how to express this quantity in different coordinate systems. Show that this same distance written in cylindrical coordinates is: \begin{equation*} \left|\vec r -\vec r\,{}'\right| =\sqrt{s^2+s\,{}'^2-2ss\,{}'\cos(\phi-\phi\,{}') +(z-z\,{}')^2} \end{equation*}
- Show that this same distance written in spherical coordinates is: \begin{equation*} \left\vert\vec r -\vec r\,{}'\right\vert =\sqrt{r'^2+r\,{}^2-2rr\,{}' \left[\sin\theta\sin\theta\,{}'\cos(\phi-\phi\,{}') +\cos\theta\cos\theta\,{}'\right]} \end{equation*}
- Now assume that \(\vec r\,{}'\) and \(\vec r\) are in the \(x\)-\(y\) plane. Simplify the previous two formulas.
- Linear Quadrupole (w/ series)
Consider a collection of three charges arranged in a line along the \(z\)-axis: charges \(+Q\) at \(z=\pm D\) and charge \(-2Q\) at \(z=0\).
Find the electrostatic potential at a point \(\vec{r}\) in the \(xy\)-plane at a distance \(s\) from the center of the quadrupole. The formula for the electrostatic potential \(V\) at a point \(\vec{r}\) due to a charge \(Q\) at the point \(\vec{r}'\) is given by: \[ V(\vec{r})=\frac{1}{4\pi\epsilon_0} \frac{Q}{\vert \vec{r}-\vec{r}'\vert} \]
Assume \(s\gg D\). Find the first two non-zero terms of a power series expansion to the electrostatic potential you found in the first part of this problem.
- A series of charges arranged in this way is called a linear quadrupole. Why?