Problem-Solving: Fall-2024
W1 D3 Practice: Due W1 D3
- Power Series Practice
- Calculate the \(n=0, 1, 2, 3, 4\) coefficients of the power series for \(\cos{z}\) expanded around \(z=\pi\). Using these coefficients, find a power series approximation for this function.
- Plot both the original function and your approximation.
- For what values of \(z\) is your approximation “good”?
- Calculate the \(n=0, 1, 2, 3, 4\) coefficients of the power series for \(\cos{z}\) expanded around \(z=\pi\). Using these coefficients, find a power series approximation for this function.
- Sensemaking from Graphs of Power Series I
- For the following graphs, identify the minimum order in a power series expansion that could accurately describe the curve for all values of the independent variable.
- For the following graphs, identify the minimum order in a power series expansion that could accurately describe the curve for all values of the independent variable.
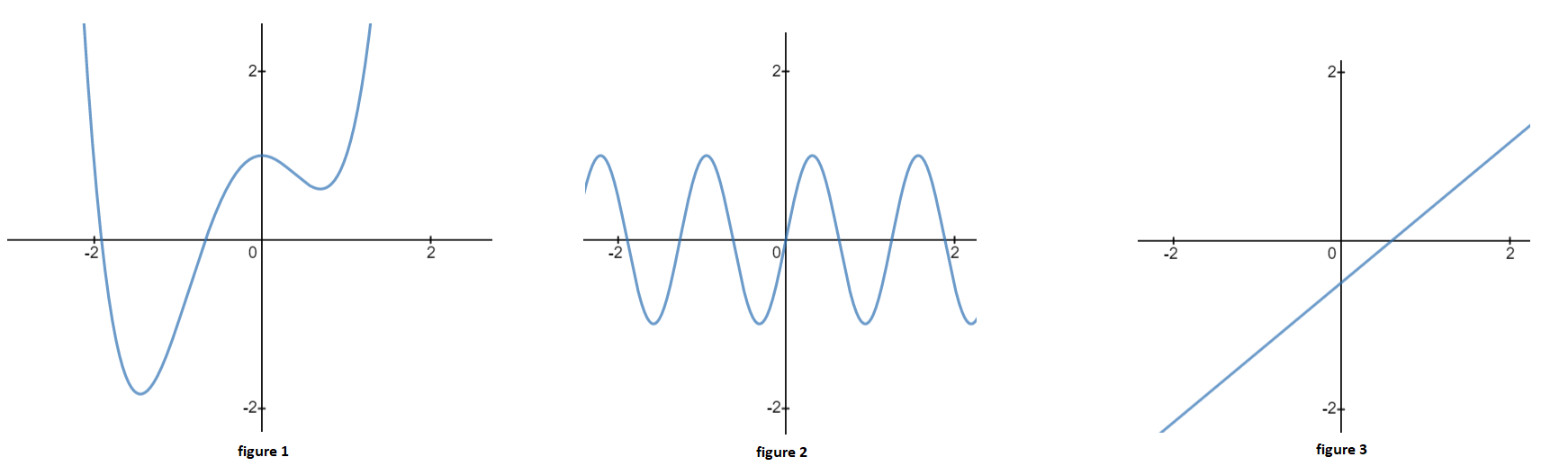
- Approximating Functions with Taylor Series
Go to The Geometry of Mathematical Methods' page on approximating power series and enter the following function into the GeoGebra applet in the figure at the bottom of the page. \begin{align} Function: \frac{7}{2}x - 3x^2 + x^3 - \frac{1}{9}x^4 +\frac{1}{180} x^5 - \frac{1}{1014} x^6 \end{align}
Answer the following questions about the above function using the applet, assuming the region where the function accurately represents a physical system is \(0 \leq x \leq 5\) (i.e. where both \(x\) and the function itself are positive).
- Set \(m=0\), then move \(a\) between \(0\) and \(5\) and describe in words what the \(m=0\) expansion order is telling you for each value of \(a\). Do the same for \(m=1\). Finally, do this for \(m=2\) and use what this series approximation does as a model to explain what will happen for expansions at all higher values of \(m\).
- Set the approximation to expand around \(x=0\). What is the minimum expansion order necessary to approximate the function within \(15\%\) of its actual value at \(x=2\)? What about within \(5\%\)? Verify these with a calculation.
- Still expanding around \(x=0\), as you go from \(m=4\) to \(m=5\), does the term you're adding have a positive or negative coefficent? How do you know?
- Still expanding around \(x=0\), as you go from \(m=4\) to \(m=5\), is your approximation improving at \(x=2\)? What about \(x=4\)? Is this the behavior you expect? Explain.