Fourier Series of a Triangle Wave

• Oscillations and Waves 2023

  In this problem, you will practice finding a Fourier series and then using it to solve a differential equation for a real physical situation. When you make plots during this problem, choose reasonable values for quantities not given, and state explicitly what they are.

  1. Find the Fourier series for a triangle wave (such as the one shown in the figure), which has amplitude \(A\) and period \(T\). Plot several approximations to your solution including the first nonzero term, the first two nonzero terms, and the first four nonzero terms. Make a histogram of your coefficients, i.e. find the spectrum.

     

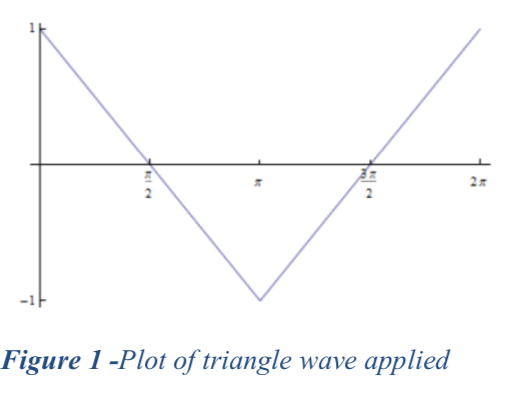
     PURELY OPTIONAL Sense-making Visualization: Plot the full triangle wave and give a brief explanation of how it compares to your previous plots.

  2. Write down the differential equation and the particular solution for a series LRC circuit that is driven by a sinusoidal voltage \(V(t) =V_0\cos(\omega t)\). You may use your previous homework solutions, but be sure to cite them!

  3. Suppose instead that the applied voltage to a series LRC circuit has the form of the triangle wave from part a. Write down the differential equation with the new applied voltage in terms of the Fourier series you found. Find \(I(t)\), the particular solution to this equation.

     PURELY OPTIONAL Sense-making Visualization: Make a plot of the current in the circuit \(I(t)\) superimposed on the applied voltage signal \(V(t)\) for three different frequencies: the resonant frequency, nine times the resonant frequency, and one-ninth of the resonant frequency. See trianagle wave mathematica file.